
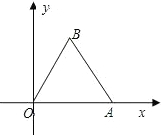
如图,边长为4的等边三角形AOB的顶点O在坐标原点,点A在x轴正半轴上,点B在第一象限.一动点P沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段BP的中点绕点P按顺时针方向旋转60°得点C,点C随点P的运动而运动,连接CP、CA,过点P作PD⊥OB于点D.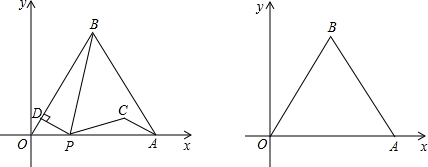
(1)填空:PD的长为 (用含t的代数式表示);
(2)求点C的坐标(用含t的代数式表示);
(3)在点P从O向A运动的过程中,△PCA能否成为直角三角形?若能,求t的值.若不能,请说明理由;
(4)填空:在点P从O向A运动的过程中,点C运动路线的长为
(1)∵△AOB是等边三角形,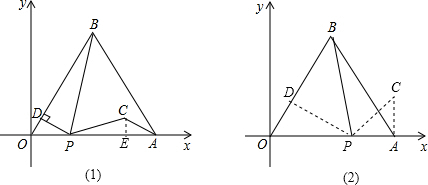
∴OB=OA=AB=4,∠BOA=∠OAB=∠ABO=60°.
∵PD⊥OB,∴∠PDO=90°,∴∠OPD=30°,∴OD=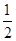 OP.∵OP=t,∴OD=
OP.∵OP=t,∴OD=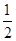 t,在Rt△OPD中,由勾股定理,得PD=
t,在Rt△OPD中,由勾股定理,得PD=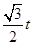
(2)如图(1)过C作CE⊥OA于E,∴∠PEC=90°,
∵OD=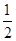 t,∴BD=4-
t,∴BD=4-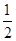 t.
t.
∵线段BP的中点绕点P按顺时针方向旋转60°得点C,
∴∠BPC=60°.∵∠OPD=30°,
∴∠BPD+∠CPE=90°.∴∠DBP=∠CPE
∴△PCE∽△BPD
∴,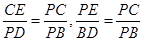
∴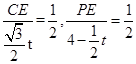 ,,
,,
∴CE=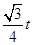 ,PE=
,PE=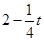 ,OE=
,OE=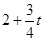 ,∴C(
,∴C(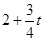 ,
,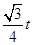 ).
).
(3)如图(3)当∠PCA=90度时,作CF⊥PA,∴△PCF∽△ACF,∴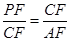 ,∴CF2=PF•AF,
,∴CF2=PF•AF,
∵PF=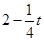 ,AF=4-OF=2-
,AF=4-OF=2- CF=
CF=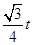 ,
,
∴( )2=(
)2=(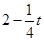 )(2-
)(2-
 ),
),
求得t=2,这时P是OA的中点.
如图(2)当∠CAP=90°时,C的横坐标就是4,
∴2+ =4∴t=
=4∴t=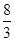
(4)设C(x,y),
∴x=2+ ,y=
,y= ,∴y=
,∴y=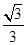 x-
x-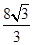 ,
,
∴C点的运动痕迹是一条线段.当t=0时,C1(2,0),当t=4时,C2(5,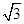 ),∴由两点间的距离公式得:C1C2=2
),∴由两点间的距离公式得:C1C2=2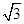 .
.
解析


科目:初中数学 来源: 题型:
 如图,边长为2的等边三角形OAB的顶点A在x轴的正半轴上,B点位于第一象限,将△OAB绕点O顺时针旋转30°后,恰好点A落在双曲线y=
如图,边长为2的等边三角形OAB的顶点A在x轴的正半轴上,B点位于第一象限,将△OAB绕点O顺时针旋转30°后,恰好点A落在双曲线y=| k | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
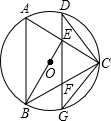 如图,边长为4的等边三角形ABC内接于⊙O,直线EF经过边AC,BC的中点,交⊙O于D、G两点.
如图,边长为4的等边三角形ABC内接于⊙O,直线EF经过边AC,BC的中点,交⊙O于D、G两点.
|
|
| p+pm |
| m |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•福州质检)如图,边长为6的等边三角形ABC中,E是对称轴AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转60°得到FC,连接DF.则在点E运动过程中,DF的最小值是
(2013•福州质检)如图,边长为6的等边三角形ABC中,E是对称轴AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转60°得到FC,连接DF.则在点E运动过程中,DF的最小值是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com