
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)![]() (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=13,则:
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=13,则: 若n=24,则第100次“F”运算的结果是________.
若n=24,则第100次“F”运算的结果是________.
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0.将第一行数字从左到右依次记为![]() ,
,![]() ,
,![]() ,
,![]() ,那么可以转换为该生所在班级序号,其序号为
,那么可以转换为该生所在班级序号,其序号为![]() .如图2第一行数字从左到右依次为0,1,0,1,序号为
.如图2第一行数字从左到右依次为0,1,0,1,序号为![]() ,表示该生为5班学生.表示6班学生的识别图案是( )
,表示该生为5班学生.表示6班学生的识别图案是( )


A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区为治理污水,需要铺设一段全长为 720 米的污水排放管道.“…”.设原计划每天铺设 x 米,可以列出方程![]() ,根据情景及所列方程,题中用“…”表示的缺失条件应补为( )
,根据情景及所列方程,题中用“…”表示的缺失条件应补为( )
A.实际施工时每天的工作效率比原计划高 20%,结果提前 2 天完成任务;
B.原计划每天的工作效率比实际施工时低 20%,结果提前 2 天完成任务;
C.实际施工时每天的工作效率比原计划高 20%,结果延后 2 天完成任务;
D.原计划每天的工作效率比实际施工时低 20%,结果延后 2 天完成任务.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上有A、B两点(点A在点B的左侧),且两点距离为12个单位长度,动点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.
![]()
(1)图中如果点A、B表示的数是互为相反数,那么点A表示的数是__________;
(2)当t=4秒时,点A与点P之间的距离是___________个长度单位;
(3)当点A表示的数是-2时,用含t的代数式表示点P表示的数;
(4)若点P到点A的距离是点P到点B的距离的2倍,请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
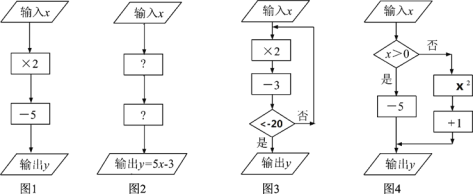
【题目】(知识背景)在学习计算框图时,可以用![]() 表示数据输入、输出框;
表示数据输入、输出框;![]() 用表示数据处理和运算框:用◇表示数据判断框(根据条件决定执行两条路径中的某一条)
用表示数据处理和运算框:用◇表示数据判断框(根据条件决定执行两条路径中的某一条)
(尝试解决)
(1)①如图1,当输入数![]() 时,输出数y=_________;
时,输出数y=_________;
②如图2,第一个“![]() ”内,应填_________;第二个“
”内,应填_________;第二个“![]() ”内,应填_________;
”内,应填_________;
(2)①如图3,当输入数![]() 时,输出数
时,输出数![]() =_________;
=_________;
②如图4,当输出的值![]() =26,则输入的值
=26,则输入的值![]() =_________;
=_________;
(实际应用)
(3)为鼓励节约用水,决定对用水实行“阶梯价”:当每月用水量不超过10吨时(含10吨),以3元/吨的价格收费;当每月用水量超过10吨时,超过部分以4元/吨的价格收费.请设计出一个“计算框图”,使得输入数为用水量![]() ,输出数为水费
,输出数为水费![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上依次有A,C,B三地,甲、乙两人同时出发,甲从A地骑自行车去B地,途经C地休息1分钟,继续按原速骑行至B地,甲到达B地后,立即按原路原速返回A地;乙步行从B地前往A地.甲、乙两人距A地的路程y(米)与时间x(分)之间的函数关系如图所示,请结合图象解答下列问题:
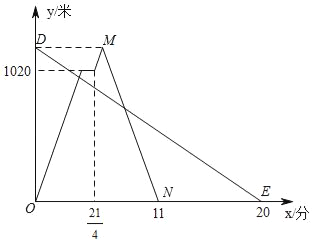
(1)请写出甲的骑行速度为 米/分,点M的坐标为 ;
(2)求甲返回时距A地的路程y与时间x之间的函数关系式(不需要写出自变量的取值范围);
(3)请直接写出两人出发后,在甲返回A地之前,经过多长时间两人距C地的路程相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一只不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20个,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,然后把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
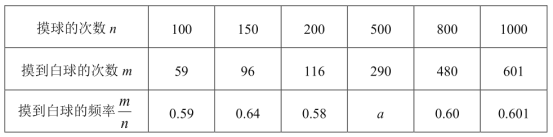
(1)上表中的a= ;
(2)“摸到白球”的概率的估计值是 (精确到0.1)
(3)试估算口袋中黑、白两种颜色的球各有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 、
、![]() 在数轴上分别表示有理数
在数轴上分别表示有理数![]() ,
,![]() ;
;
(1)对照数轴填写下表:
| 6 | -1 | -2 | 4 |
| 4 | -5 | 3 | -4 |
|
(2)若![]() 、
、![]() 两点间的距离记为
两点间的距离记为![]() ,试问:
,试问:![]() 和
和![]() ,
,![]() 有何数量关系?
有何数量关系?
(3)写出所有符合条件的整数点![]() ,使它到10和-10的距离之和为span>20,并求所有这些整数的数的和;
,使它到10和-10的距离之和为span>20,并求所有这些整数的数的和;
(4)找出(3)中满足到10和-10的距离之差大于1而小于5的整数的点![]() ;
;
(5)若点![]() 表示的数为
表示的数为![]() ,当点
,当点![]() 在什么位置时,
在什么位置时,![]() 取得的值最小,并求出这个最小值.
取得的值最小,并求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
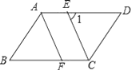
【题目】如图,在ABCD中,CE平分∠BCD,且交AD于点E,AF∥CE,且交BC于点F.
(1)求证:△ABF≌△CDE;
(2)如图,若∠B=52°,求∠1的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com