
【题目】如图,已知△ABC中,AB=AC,利用直尺和圆规,根据下列要求作图(保留作图痕迹,不要求写作法),并根据要求填空:
(1)作∠B的平分线BD,交AC于点D;
(2)作线段AB的垂直平分线EF,交AB于点E,交AC于点F;
(3)如果点F与点D重合,则∠A= °.

【答案】(1)见解析;(2)见解析;(3)36°
【解析】
(1)以B为圆心,以任意长度为半径作弧,分别交AB、BC与M、N,分别以M、N为圆心,以大于![]() MN为半径作弧,连接B和两弧的交点并延长交AC于D,BD即为所求;
MN为半径作弧,连接B和两弧的交点并延长交AC于D,BD即为所求;
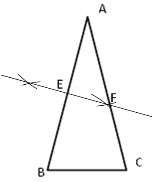
(2)分别以A、B为圆心,以大于![]() AB为半径作弧,连接两弧的两个交点交AB于E,交AC于F,EF即为所求;
AB为半径作弧,连接两弧的两个交点交AB于E,交AC于F,EF即为所求;
(3)根据等边对等角可得:∠ABC=∠ACB,再根据角平分线的定义可得:∠ABC=2∠ABF,然后根据垂直平分线的性质和等边对等角可得:∠FBA=∠A,从而得出∠ACB=∠ABC=2∠A,最后根据三角形的内角和定理列方程即可求出∠A.
解:(1)以B为圆心,以任意长度为半径作弧,分别交AB、BC与M、N,分别以M、N为圆心,以大于![]() MN为半径作弧,连接B和两弧的交点并延长交AC于D,如下图所示,BD即为所求;
MN为半径作弧,连接B和两弧的交点并延长交AC于D,如下图所示,BD即为所求;
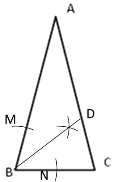
(2)分别以A、B为圆心,以大于![]() AB为半径作弧,连接两弧的两个交点交AB于E,交AC于F,如下图所示EF即为所求;
AB为半径作弧,连接两弧的两个交点交AB于E,交AC于F,如下图所示EF即为所求;
(3)当F、D重合时,如下图所示,
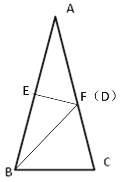
∵AB=AC
∴∠ABC=∠ACB
∵BF平分∠ABC
∴∠ABC=2∠ABF
∵EF垂直平分AB
∴FB=FA
∴∠FBA=∠A
∴∠ACB=∠ABC=2∠A
∵∠ACB+∠ABC+∠A=180°
∴2∠A+2∠A+∠A=180°
解得:∠A=36°


科目:初中数学 来源: 题型:
【题目】如图所示,在完全重合放置的两张矩形纸片![]() 中,
中,![]() ,
,![]() ,将上面的矩形纸片折叠,使点
,将上面的矩形纸片折叠,使点![]() 与点
与点![]() 重合,折痕为
重合,折痕为![]() ,点
,点![]() 的对应点为
的对应点为![]() ,连接
,连接![]() ,则图中阴影部分的面积为( )
,则图中阴影部分的面积为( )

A. ![]() B. 6 C.
B. 6 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一条直线分割一个三角形,如果能分割出等腰三角形,那么就称这条直线为该三角形的一条等腰分割线.在直角三角形ABC中,∠C=90°,AC=8,BC=6.

(1)如图(1),若 O 为 AB 的中点,则直线 OC_____△ABC 的等腰分割线(填“是”或“不是”)
(2)如图(2)已知△ABC 的一条等腰分割线 BP 交边 AC 于点 P,且 PB=PA,请求出 CP 的长度.
(3)如图(3),在△ABC 中,点 Q 是边 AB 上的一点,如果直线 CQ 是△ABC 的等腰分割线,求线段BQ 的长度等于 ______.(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在一个长方形的草坪ABCD中,修了一条A-E-C的小路.AB=12米,BC=16米,AE=11米.极个别同学为了走“捷径”,沿着AC路线行走,破坏草坪.
(1)请求出小路EC段的长度;
(2)请求出实际上这些同学仅仅少走了多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与
的图象与![]() 轴、
轴、![]() 轴交于
轴交于![]() 、
、![]() 两点,与反比例函数
两点,与反比例函数![]() 的图象相交于
的图象相交于![]() 、
、![]() 两点,分别过
两点,分别过![]() 、
、![]() 两点作
两点作![]() 轴,
轴,![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() 、
、![]() ,连接
,连接![]() 、
、![]() ,有下列结论:①
,有下列结论:①![]() 与
与![]() 的面积相等;②
的面积相等;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 的面积等于
的面积等于![]() ,其中正确的个数有( )
,其中正确的个数有( )
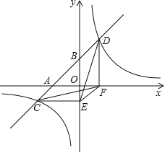
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从不同的方向看同一物体时,可能看到不同的图形.其中,从正面看到的图叫主视图,从左面看到的图叫左视图,从上面看到的图叫俯视图.由若干个(大于![]() 个)大小相同的正方体组成一个几何体的主视图和俯视图如图所示,则这个几何体的左视图不可能是( )
个)大小相同的正方体组成一个几何体的主视图和俯视图如图所示,则这个几何体的左视图不可能是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com