
ФЪЦұҪЗМЭРО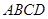 ЦР,
ЦР,  , ёЯ
, ёЯ (ИзНј1). ¶Ҝөг
(ИзНј1). ¶Ҝөг Н¬КұҙУөг
Н¬КұҙУөг іц·ў, өг
іц·ў, өг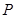 СШ
СШ ФЛ¶ҜөҪөг
ФЛ¶ҜөҪөг НЈЦ№, өг
НЈЦ№, өг СШ
СШ ФЛ¶ҜөҪөг
ФЛ¶ҜөҪөг НЈЦ№,БҪөгФЛ¶ҜКұөДЛЩ¶И¶јКЗ1cm/s,¶шөұөг
НЈЦ№,БҪөгФЛ¶ҜКұөДЛЩ¶И¶јКЗ1cm/s,¶шөұөг өҪҙпөг
өҪҙпөг Кұ,өг
Кұ,өг ХэәГөҪҙпөг
ХэәГөҪҙпөг . Йи
. Йи Н¬КұҙУөг
Н¬КұҙУөг іц·ў,ҫӯ№эөДКұјдОӘ
іц·ў,ҫӯ№эөДКұјдОӘ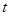 (s)Кұ,
(s)Кұ,  өДГж»эОӘ
өДГж»эОӘ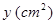 (ИзНј2). ·ЦұрТФ
(ИзНј2). ·ЦұрТФ ОӘәбЎўЧЭЧшұкҪЁБўЦұҪЗЧшұкПө, ТСЦӘөг
ОӘәбЎўЧЭЧшұкҪЁБўЦұҪЗЧшұкПө, ТСЦӘөг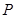 ФЪ
ФЪ ұЯЙПҙУ
ұЯЙПҙУ өҪ
өҪ ФЛ¶ҜКұ,
ФЛ¶ҜКұ,  Ул
Ул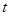 өДәҜКэНјПуКЗНј3ЦРөДПЯ¶О
өДәҜКэНјПуКЗНј3ЦРөДПЯ¶О .
.

(Нј1) (Нј2) (Нј3)
ЈЁ1Ј©·ЦұрЗуіцМЭРОЦР өДіӨ¶И;
өДіӨ¶И;
ЈЁ2Ј©·ЦұрРҙіцөг ФЪ
ФЪ ұЯЙПәН
ұЯЙПәН ұЯЙПФЛ¶ҜКұ,
ұЯЙПФЛ¶ҜКұ,  Ул
Ул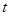 өДәҜКэ№ШПөКҪ(ЧўГчЧФұдБҝөДИЎЦө·¶О§), ІўФЪНј3ЦРІ№И«ХыёцФЛ¶ҜЦР
өДәҜКэ№ШПөКҪ(ЧўГчЧФұдБҝөДИЎЦө·¶О§), ІўФЪНј3ЦРІ№И«ХыёцФЛ¶ҜЦР №ШУЪ
№ШУЪ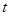 өДәҜКэ№ШПөөДҙуЦВНјПу.
өДәҜКэ№ШПөөДҙуЦВНјПу.
ЈЁ3Ј©ОКЈәКЗ·сҙжФЪХвСщөДt,К№PQҪ«МЭРОABCDөДГж»эЗЎәГ·ЦіЙ1:6өДБҪІҝ·ЦЈҝИфҙжФЪ,ЗуіцХвСщөДtөДЦөЈ»ИфІ»ҙжФЪ,ЗлЛөГчАнУЙЈ®
ЈЁ1Ј© Ј»
Ј»
ЈЁ2Ј©өұөг ФЪ
ФЪ ЙПКұ,
ЙПКұ,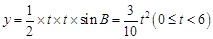 Ј»өұөг
Ј»өұөг ФЪ
ФЪ ЙПКұ,
ЙПКұ,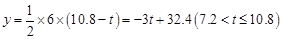 Ј»НјПујыҪвОцЈ»
Ј»НјПујыҪвОцЈ»
ЈЁ3Ј© »т6.
»т6.
ҪвОцКФМв·ЦОцЈәЈЁ1Ј©PФЪADұЯЙПФЛ¶ҜКұ,ИэҪЗРОBQPТФBQОӘөЧұЯ,ТФCDөДіӨОӘёЯ,ТтҙЛҝЙёщҫЭИэҪЗРОBQPөДГж»э,ЗуіцBC,¶шPЎўQЛЩ¶ИПаН¬,PөҪAөДКұјдУлQөҪCөДКұјдПаН¬,ТтҙЛBA=BCЈ®ЗуADөДіӨҝЙНЁ№э№№ҪЁЦұҪЗИэҪЗРОАҙЗуҪвЈ®
ЈЁ2Ј©ИэҪЗРОBQPЦР,BQ=t,BP=t,ТФBQОӘөЧұЯөДёЯ,ҝЙУГBP•sinBАҙұнКҫ,И»әуҝЙёщҫЭИэҪЗРОөДГж»эјЖЛ㹫КҪөГіц№ШУЪy,tөДәҜКэ№ШПөКҪЈ®
ЈЁ3Ј©PQҪ«МЭРОABCDөДГж»э·ЦіЙБҪІҝ·Ц,ЧуұЯІҝ·ЦГж»эЦрҪҘФцҙу,УТұЯГж»эЦрҪҘјхЙЩ,№КУРБҪЦЦҝЙДЬ,Т»КЗЧуұЯГж»эөИУЪМЭРОABCDГж»эөД ,БнТ»ЦЦКЗУТұЯГж»эөИУЪМЭРОABCDГж»эөД
,БнТ»ЦЦКЗУТұЯГж»эөИУЪМЭРОABCDГж»эөД .
.
КФМвҪвОцЈәЈЁ1Ј©Йи¶Ҝөгіц·ўtГләу,өгPөҪҙпөгAЗТөгQХэәГөҪҙпөгCКұ,BC=BA=t,
ФтSЎчBPQ=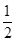 ЎБtЎБ3.6=10.8,
ЎБtЎБ3.6=10.8,
ЛщТФt=6ЈЁГлЈ©Ј®
ФтBA=6ЈЁcmЈ©,
№эөгAЧчAHЎНBCУЪH,
ФтЛДұЯРОAHCDКЗҫШРО,
ЎаAD=CH,CD=AH=3.6cm,
ФЪRtЎчABHЦР,BH= cm,
cm,
ЎаCH=1.2cm,
ЎаAD=1.2cmЈ»
ЈЁ2Ј©өұөг ФЪ
ФЪ ЙПКұ,
ЙПКұ,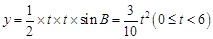 Ј»
Ј»
өұөг ФЪ
ФЪ ЙПКұ,
ЙПКұ,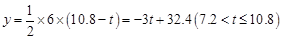 ;
;
ХыёцФЛ¶ҜЦР №ШУЪ
№ШУЪ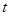 өДәҜКэ№ШПөөДҙуЦВНјПуЈә
өДәҜКэ№ШПөөДҙуЦВНјПуЈә
ЈЁ3Ј©МЭРОABCDөДГж»эЈә
ЙиҙжФЪХвСщөДt,К№PQҪ«МЭРОABCDөДГж»эЗЎәГ·ЦіЙ1:6өДБҪІҝ·Ц,
өұөг ФЪ
ФЪ ЙПКұ,ЎчPQBөДГж»эКЗЈә
ЙПКұ,ЎчPQBөДГж»эКЗЈә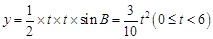 ,№КУРЈә
,№КУРЈә ,ҙЛКұЈә
,ҙЛКұЈә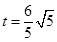 ;
;
өұөг Улөг
Улөг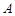 ЙПЦШәПКұ,өг
ЙПЦШәПКұ,өг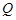 Улөг
Улөг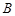 ЙПЦШәП,ЎчPQBөДГж»эКЗЈә
ЙПЦШәП,ЎчPQBөДГж»эКЗЈә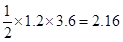 ,ҙЛКұЈә
,ҙЛКұЈә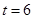 ,ТІВъЧгPQҪ«МЭРОABCDөДГж»эЗЎәГ·ЦіЙ1:6өДБҪІҝ·Ц.ЛщТФЈә
,ТІВъЧгPQҪ«МЭРОABCDөДГж»эЗЎәГ·ЦіЙ1:6өДБҪІҝ·Ц.ЛщТФЈә »т6.
»т6.
ҝјөгЈә¶юҙОәҜКэЧЫәПМвЈ®



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
ТСЦӘ¶юҙОәҜКэy=x2©Ғ2mx+4m©Ғ8ЈЁ1Ј©өұxЎЬ2КұЈ¬әҜКэЦөyЛжxөДФцҙу¶шјхРЎЈ¬ЗуmөДИЎЦө·¶О§Ј®ЈЁ2Ј©ТФЕЧОпПЯy=x2©Ғ2mx+4m©Ғ8өД¶ҘөгAОӘТ»ёц¶ҘөгЧчёГЕЧОпПЯөДДЪҪУХэИэҪЗРОAMNЈЁMЈ¬NБҪөгФЪ’ҒОпПЯЙПЈ©Ј¬ЗлОКЈәЎчAMNөДГж»эКЗУлmОЮ№ШөД¶ЁЦөВрЈҝИфКЗЈ¬ЗлЗуіцХвёц¶ЁЦөЈ»ИфІ»КЗЈ¬ЗлЛөГчАнУЙЈ®ЈЁ3Ј©ИфЕЧОпПЯy=x2©Ғ2mx+4m©Ғ8УлxЦбҪ»өгөДәбЧшұкҫщОӘХыКэЈ¬ЗуХыКэmөДЧоРЎЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
ДіЙМИЛИз№ыҪ«Ҫш»хјЫОӘ8ФӘөДЙМЖ·°ҙГҝјю10ФӘіцКЫЈ¬ГҝМмҝЙПъКЫ100јюЈ¬ПЦІЙУГМбёЯКЫіцјЫЈ¬јхЙЩҪш»хБҝөД°м·ЁФцјУАыИуЈ¬ТСЦӘХвЦЦЙМЖ·ГҝХЗјЫ1ФӘЖдПъКЫБҝҫНТӘјхЙЩ10јюЈ¬ОКЛыҪ«КЫіцјЫx¶ЁОӘ¶аЙЩФӘКұЈ¬ІЕДЬК№ГҝМмЛщЧ¬өДАыИуy ЧоҙуЈҝІўЗуіцЧоҙуАыИуЎЈ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
ИзНј,ФЪЖҪГжЦұҪЗЧшұкПөЦР,¶ҘөгОӘЈЁ4,1Ј©өДЕЧОпПЯҪ» ЦбУЪөг
ЦбУЪөг ,Ҫ»
,Ҫ» ЦбУЪ
ЦбУЪ ,
, БҪөгЈЁөг
БҪөгЈЁөг ФЪөг
ФЪөг өДЧуІаЈ©,ТСЦӘ
өДЧуІаЈ©,ТСЦӘ өгЧшұкОӘЈЁ6,0Ј©.
өгЧшұкОӘЈЁ6,0Ј©.
ЈЁ1Ј©ЗуҙЛЕЧОпПЯөДҪвОцКҪЈ»
ЈЁ2Ј©БӘҪбAB,№эөг ЧчПЯ¶О
ЧчПЯ¶О өДҙ№ПЯҪ»ЕЧОпПЯУЪөг
өДҙ№ПЯҪ»ЕЧОпПЯУЪөг ,Из№ыТФөг
,Из№ыТФөг ОӘФІРДөДФІУлЕЧОпПЯөД¶ФіЖЦб
ОӘФІРДөДФІУлЕЧОпПЯөД¶ФіЖЦб ПаЗР,ПИІ№И«НјРО,ФЩЕР¶ПЦұПЯ
ПаЗР,ПИІ№И«НјРО,ФЩЕР¶ПЦұПЯ УлЎС
УлЎС өДО»ЦГ№ШПөІўјУТФЦӨГчЈ»
өДО»ЦГ№ШПөІўјУТФЦӨГчЈ»
ЈЁ3Ј©ТСЦӘөг КЗЕЧОпПЯЙПөДТ»ёц¶Ҝөг,ЗТО»УЪ
КЗЕЧОпПЯЙПөДТ»ёц¶Ҝөг,ЗТО»УЪ ,
, БҪөгЦ®јд.ОКЈәөұөг
БҪөгЦ®јд.ОКЈәөұөг ФЛ¶ҜөҪКІГҙО»ЦГКұ,
ФЛ¶ҜөҪКІГҙО»ЦГКұ, өДГж»эЧоҙуЈҝЗуіц
өДГж»эЧоҙуЈҝЗуіц өДЧоҙуГж»э.
өДЧоҙуГж»э.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
ТСЦӘЦұПЯ ·ЦұрУлyЦбЎўxЦбПаҪ»УЪAЎўBБҪөгЈ¬Ул¶юҙОәҜКэ
·ЦұрУлyЦбЎўxЦбПаҪ»УЪAЎўBБҪөгЈ¬Ул¶юҙОәҜКэ өДНјПсҪ»УЪAЎўCБҪөгЈ®
өДНјПсҪ»УЪAЎўCБҪөгЈ®
(1)өұөгCЧшұкОӘЈЁ Ј¬
Ј¬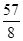 Ј©КұЈ¬ЗуЦұПЯABөДҪвОцКҪЈ»
Ј©КұЈ¬ЗуЦұПЯABөДҪвОцКҪЈ»
(2)ФЪЈЁ1Ј©ЦРЈ¬ИзНјЈ¬Ҫ«ЎчABOСШyЦб·ӯХЫ180ЎгЈ¬ИфөгBөД¶ФУҰөгDЗЎәГВдФЪ¶юҙОәҜКэ өДНјПсЙПЈ¬ЗуөгDөҪЦұПЯABөДҫаАлЈ»
өДНјПсЙПЈ¬ЗуөгDөҪЦұПЯABөДҫаАлЈ»
(3)өұ-1ЎЬxЎЬ1КұЈ¬¶юҙОәҜКэ УРЧоРЎЦө-3,ЗуКөКэmөДЦө.
УРЧоРЎЦө-3,ЗуКөКэmөДЦө.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
ТСЦӘЈ¬№ШУЪxөД¶юҙОәҜКэЈ¬ ЈЁkОӘХэХыКэЈ©.
ЈЁkОӘХэХыКэЈ©.
ЈЁ1Ј©Иф¶юҙОәҜКэ өДНјПуУлxЦбУРБҪёцҪ»өгЈ¬ЗуkөДЦө.
өДНјПуУлxЦбУРБҪёцҪ»өгЈ¬ЗуkөДЦө.
ЈЁ2Ј©Иф№ШУЪxөДТ»ФӘ¶юҙО·ҪіМ ЈЁkОӘХэХыКэЈ©УРБҪёцІ»ПаөИөДХыКэҪвЈ¬өгAЈЁmЈ¬y1Ј©Ј¬BЈЁm+1Ј¬y2Ј©Ј¬CЈЁm+2Ј¬y3Ј©¶јФЪ¶юҙОәҜКэ
ЈЁkОӘХэХыКэЈ©УРБҪёцІ»ПаөИөДХыКэҪвЈ¬өгAЈЁmЈ¬y1Ј©Ј¬BЈЁm+1Ј¬y2Ј©Ј¬CЈЁm+2Ј¬y3Ј©¶јФЪ¶юҙОәҜКэ ЈЁkОӘХэХыКэЈ©НјПуЙПЈ¬ЗуК№y1ЎЬy2ЎЬy3іЙБўөДmөДИЎЦө·¶О§.
ЈЁkОӘХэХыКэЈ©НјПуЙПЈ¬ЗуК№y1ЎЬy2ЎЬy3іЙБўөДmөДИЎЦө·¶О§.
ЈЁ3Ј©Ҫ«ЈЁ2Ј©ЦРөДЕЧОпПЯЖҪТЖЈ¬өұ¶ҘөгЦБФӯөгКұЈ¬ЦұПЯy=2x+bҪ»ЕЧОпПЯУЪA(-1Ј¬n)ЎўB(2Ј¬t)БҪөгЈ¬ОКФЪyЦбЙПКЗ·сҙжФЪТ»өгCЈ¬К№өГЎчABCөДДЪРДФЪyЦбЙП.ИфҙжФЪЈ¬ЗуіцөгCөДЧшұкЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙ.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
ТСЦӘЕЧОпПЯ ЈЁmКЗіЈКэЈ¬
ЈЁmКЗіЈКэЈ¬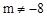 Ј©УлxЦбУРБҪёцІ»Н¬өДҪ»өгAЎўBЈ¬өгAЎўөгB№ШУЪЦұПЯx=1¶ФіЖЈ¬ЕЧОпПЯөД¶ҘөгОӘC.
Ј©УлxЦбУРБҪёцІ»Н¬өДҪ»өгAЎўBЈ¬өгAЎўөгB№ШУЪЦұПЯx=1¶ФіЖЈ¬ЕЧОпПЯөД¶ҘөгОӘC.
ЈЁ1Ј©ҙЛЕЧОпПЯөДҪвОцКҪЈ»
ЈЁ2Ј©ЗуөгAЎўBЎўCөДЧшұк.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
ДіЙМИЛИз№ыҪ«Ҫш»хјЫОӘ8ФӘөДЙМЖ·°ҙГҝјю10ФӘіцКЫЈ¬ГҝМмҝЙПъКЫ100јюЈ¬ПЦІЙУГМбёЯКЫіцјЫЈ¬јхЙЩҪш»хБҝөД°м·ЁФцјУАыИуЈ¬ТСЦӘХвЦЦЙМЖ·ГҝХЗјЫ1ФӘЖдПъКЫБҝҫНТӘјхЙЩ10јюЈ¬ОКЛыҪ«КЫіцјЫ¶ЁОӘ¶аЙЩФӘКұЈ¬ІЕДЬК№ГҝМмЛщЧ¬өДАыИуЧоҙуЈҝІўЗуіцЧоҙуАыИуЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
ТСЦӘЈәИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПө ЦРЈ¬ЕЧОпПЯ
ЦРЈ¬ЕЧОпПЯ №эөгAЈЁ6Ј¬0Ј©әНөгBЈЁ3Ј¬
№эөгAЈЁ6Ј¬0Ј©әНөгBЈЁ3Ј¬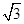 Ј©Ј®
Ј©Ј®
ЈЁ1Ј©ЗуЕЧОпПЯ өДҪвОцКҪЈ»
өДҪвОцКҪЈ»
ЈЁ2Ј©Ҫ«ЕЧОпПЯ СШxЦб·ӯХЫөГЕЧОпПЯ
СШxЦб·ӯХЫөГЕЧОпПЯ Ј¬ЗуЕЧОпПЯ
Ј¬ЗуЕЧОпПЯ өДҪвОцКҪЈ»
өДҪвОцКҪЈ»
ЈЁ3Ј©ФЪЈЁ2Ј©өДМхјюПВЈ¬ЕЧОпПЯ ЙПКЗ·сҙжФЪөгMЈ¬К№
ЙПКЗ·сҙжФЪөгMЈ¬К№ Ул
Ул ПаЛЖЈҝИз№ыҙжФЪЈ¬ЗуіцөгMөДЧшұкЈ»Из№ыІ»ҙжФЪЈ¬ЛөГчАнУЙЈ®
ПаЛЖЈҝИз№ыҙжФЪЈ¬ЗуіцөгMөДЧшұкЈ»Из№ыІ»ҙжФЪЈ¬ЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com