
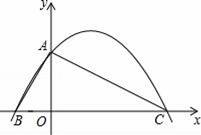
��֪����ͼ����ƽ��ֱ������ϵ�У���ABC�ı�BC��x���ϣ�����A��y����������ϣ�OA=2��OB=1��OC=4��
��1�����A��B��C����������ߵĽ���ʽ��
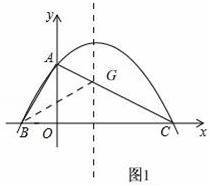
��2�����G�ǶԳ�����һ�㣬��GAB�ܳ���Сʱ����G�����ꣻ
��3���������߶Գ��ύx���ڵ�P����ƽ��ֱ������ϵ�У��Ƿ���ڵ�Q��ʹ��PAQ����PAΪ���ĵ���ֱ�������Σ������ڣ�д�����з��������ĵ�Q�����꣬��ѡ������һ���ļ���˵�����������ڣ�˵�����ɣ�
��4�����M��x���ϵĶ��㣬���ʣ���ƽ��ֱ������ϵ�У��Ƿ���ڵ�N��ʹ���Ե�A��B��M��NΪ������ı��������Σ������ڣ�ֱ��д����N�����ꣻ�������ڣ�˵�����ɣ�

�����㡿���κ����ۺ��⣮
����������1�����߶γ����������������꣬���ô���ϵ������⼴�ɣ�
��2���ҵ���B���������߶Գ���ĶԳƵ�A��ȡAB�������߶Գ���Ľ��㼴�ɣ�
��3���ֱ����P��A��AP�Ĵ��ߣ�ȡ��Q�����ݵ���ֱ�������ι���ȫ�������μ�����⣻
��4��������ABΪ�ߺ���ABΪ�Խ��߽������ۣ�������ε����ʽ�����⼴�ɣ�
����𡿽⣺��1�����������A��0��2����B����1��0������C������Ϊ��4��0����
���A��B��C����������ߵĽ���ʽΪy=a��x��4����x+1����
�ѵ�A��0��2�����룬��ã�a=��
 ��
��
���������ߵĽ���ʽΪ��y=��
 ��x��4����x+1��=
��x��4����x+1��=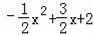
 ��
��
��2����ͼ1

����y=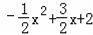
 �ĶԳ���Ϊ��x=
�ĶԳ���Ϊ��x=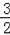
 ��
��
�ɵ�C�ǵ�B����ֱ�ߣ�x=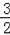
 �ĶԳƵ㣬����ֱ��AC��ֱ��x=
�ĶԳƵ㣬����ֱ��AC��ֱ��x=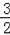
 �Ľ��㼴Ϊ��GAB�ܳ���Сʱ�ĵ�G��
�Ľ��㼴Ϊ��GAB�ܳ���Сʱ�ĵ�G��
��ֱ��AC�Ľ���ʽΪ��y=mx+n����A��0��2������C��4��0������ã���
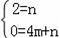
 ��
��
��ã�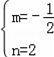
 ��
��
���ԣ�y=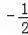
 x+2��
x+2��
��x=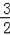
 ʱ��y=
ʱ��y=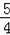
 ��
��
���Դ�ʱ��G��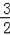
 ��
��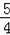
 ����
����
��3����ͼ2
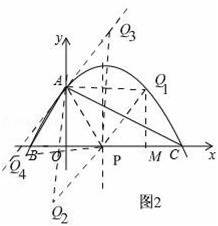

ʹ��PAQ����PAΪ���ĵ���ֱ�������ε����з��������ĵ�Q�����꣺Q1��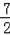
 ��
��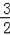
 ����Q2��
����Q2��
 ����
����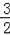
 ����Q3��2��
����Q3��2��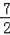
 ����Q4����2��
����Q4����2��
 ����
����
֤��Q1������Q1��Q1M��x�ᣬ����ΪM��
�����⣺��APQ1=90�㣬AP=PQ1��
���APO+��MPQ1=90�㣬
�ߡ�APO+��PAO=90�㣬
���PAO=��MPQ1��
�ڡ�AOP�͡�MPQ1�У�
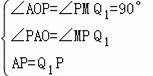
 ��
��
���AOP�ա�MPQ1��
��PM=AO=2��Q1M=OP=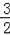
 ��
��
��OM=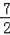
 ��
��
��ʱ��Q������Ϊ����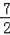
 ��
��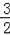
 ����
����
��4������
��N����������0����2������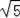
 ��2��������
��2��������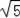
 ��2������
��2������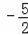
 ��2����
��2����
��������������Ҫ������κ������ۺ����⣬�����ô���ϵ������������ʽ����϶ԳƵ����߶κ���С���⣻��Ϥ����ֱ�������ε����ʣ���Ӧ���ڵ�Ĵ��ڵ��о�����Ϥ���ε����ʣ������������ζ���Ĵ������о��ǽ������Ĺؼ���
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
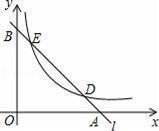
��ֱ֪��l�ֱ���x�ᡢy�ύ��A��B���㣬��˫����y=
 ��m��0��x��0���ֱ���D��E���㣬����D������Ϊ��4��1������E������Ϊ��1��n��
��m��0��x��0���ֱ���D��E���㣬����D������Ϊ��4��1������E������Ϊ��1��n��
��1���ֱ����ֱ��l��˫���ߵĽ���ʽ��
��2�����EOD�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪������y=x2+bx+c��x�ύ��A��B���㣨A����B����ࣩ����y�ύ���C��0����3�����Գ�����ֱ��x=1��ֱ��BC�������ߵĶԳ��ύ���D��
��1���������ߵĺ�����ϵʽ��
��2����ƽ����x���ֱ���������߽��ڵ�M��N��M����N����ࣩ����MNΪֱ����Բ��x�����У����Բ�İ뾶��
��3������M�ڵ������ޣ���MN��y��Ľ���Ϊ��F����C���ڵ�F�ĶԳƵ�Ϊ��E��
�ٵ��߶�MN=
 ABʱ����tan��CED��ֵ��
ABʱ����tan��CED��ֵ��
�ڵ���C��D��EΪ�������������ֱ��������ʱ����ֱ��д����M�����꣮


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
һ�����ݣ�0��1��2��3��3��5��5��10����λ���ǣ�������
A��2.5 B��3 C��3.5 D��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
ij������Ʒר��������7�������9�������������Ϊ355Ԫ������10�������20�������������Ϊ650Ԫ��
��1����ÿ�������ÿ���������������
��2����֪ÿ������Ľ���Ϊ200Ԫ��ÿ������Ľ���Ϊ160Ԫ������ר����ƻ��ò�����17400Ԫ�������������100������Ҫ��������������������������һ�룬����Ϊר������Ʒ���Ҫ��Ľ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����ͼ��ʾ��A��B��C��������ͼ�����������һ�Ѷ��ӣ�����������������Ŀ����������A��B��C����


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��ƽ��ֱ������ϵ�У���A��B��C��x���ϣ���D��E��y���ϣ�OA=OD=2��OC=OE=4��DB��DC��ֱ��AD�뾭��B��E��C����������߽���F��G���㣬����Գ��ύ��M����PΪ�߶�FG��һ�����㣨��F��G���غϣ���PQ��y���������߽��ڵ�Q��
��1����B��E��C����������ߵĽ���ʽ��
��2���Ƿ���ڵ�P��ʹ����P��Q��MΪ��������������AOD���ƣ������ڣ�������������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
��3���������ߵĶ���ΪN������QN��̽���ı���PMNQ����״�����ܷ��Ϊ���Σ����ܷ��Ϊ�������Σ����ܣ���ֱ��д����P�����ꣻ�����ܣ���˵�����ɣ�


�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com