
【题目】已知直线![]() 的图象如图所示;
的图象如图所示;
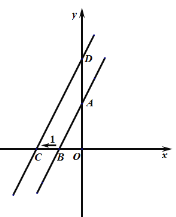
(1)直线与![]() 轴交点
轴交点![]() 的坐标是_____、与
的坐标是_____、与![]() 轴交点
轴交点![]() 的坐标______;
的坐标______;
(2)将直线![]() 沿
沿![]() 轴负半轴方向平移1个单位后得到直线
轴负半轴方向平移1个单位后得到直线![]() ,求直线与
,求直线与![]() 轴的交点
轴的交点![]() 的坐标;
的坐标;
【答案】(1)(0,2);(-1,0);(2)(0,4)
【解析】
(1)当x=0时,y=2;当y=0时,x=-1,即可求出点A和点B的坐标;
(2)根据题意,设直线CD的解析式为y=2x+b,点C的坐标为(-2,0),然后利用待定系数法即可求出直线CD的解析式,从而求出结论.
解:(1)当x=0时,y=2;当y=0时,x=-1
∴点A的坐标为(0,2),点B的坐标为(-1,0)
故答案为:(0,2);(-1,0);
(2)∵将直线![]() 沿
沿![]() 轴负半轴方向平移1个单位后得到直线
轴负半轴方向平移1个单位后得到直线![]() ,
,
∴设直线CD的解析式为y=2x+b,点C的坐标为(-2,0)
将(-2,0)代入解析式中,可得
0=-4+b
解得:b=4
∴直线CD的解析式为y=2x+4
当x=0时,y=4
∴点D的坐标为(0,4).


科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,![]() 是坐标原点,抛物线
是坐标原点,抛物线![]() 交
交![]() 轴于
轴于![]() 两点(如图),顶点是
两点(如图),顶点是![]() ,对称轴交
,对称轴交![]() 轴于点
轴于点![]()
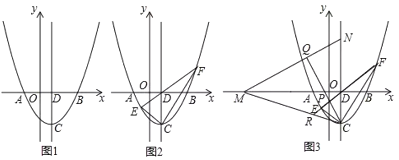
(1)如图(1)求抛物线的解析式;
(2)如图(2)![]() 是第三象限抛物线上一点,连接
是第三象限抛物线上一点,连接![]() 并延长交抛物线于点
并延长交抛物线于点![]() ,连接
,连接![]() 求证:
求证:![]() ;
;
(3)如图(3)在(2)问条件下,![]() 分别是线段
分别是线段![]() 延长线上一点,连接
延长线上一点,连接![]() ,过点
,过点![]() 作
作![]() 于
于![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,若
,若![]()
![]()
![]() 求点
求点![]() 坐标.
坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
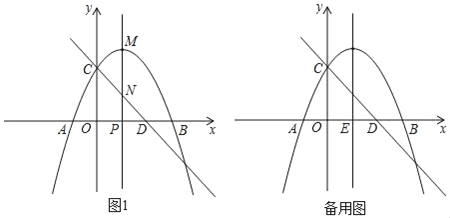
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),点
的左侧),点![]() 的坐标为
的坐标为![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .动点
.动点![]() 在抛物线上运动,过点
在抛物线上运动,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)求抛物线的解析式;
(2)当点![]() 在线段
在线段![]() 上时,
上时,![]() 的面积是否存在最大值,若存在,请求出最大值;若不存在,请说明理由;
的面积是否存在最大值,若存在,请求出最大值;若不存在,请说明理由;
(3)点![]() 是抛物线对称轴与
是抛物线对称轴与![]() 轴的交点,点
轴的交点,点![]() 是
是![]() 轴上一动点,点
轴上一动点,点![]() 在运动过程中,若以
在运动过程中,若以![]() 为顶点的四边形是平行四边形时,请直接写出点
为顶点的四边形是平行四边形时,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
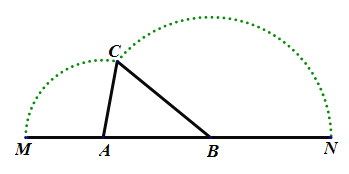
【题目】如图,已知![]() 是线段
是线段![]() 上的两点,
上的两点,![]() ,
,![]() ,
,![]() .以
.以![]() 为圆心以
为圆心以![]() 为半径作圆弧,以
为半径作圆弧,以![]() 为圆心以
为圆心以![]() 为半径作圆弧,两圆弧相交于点
为半径作圆弧,两圆弧相交于点![]() 构成
构成![]() ,设
,设![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)若![]() 为直角三角形,求
为直角三角形,求![]() 的值;
的值;
(3)当![]() 是锐角时,求
是锐角时,求![]() 的最大面积?
的最大面积?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某斜拉桥引申出的部分平面图,AE,CD是两条拉索,其中拉索CD与水平桥面BE的夹角为72°,其底端与立柱AB底端的距离BD为4米,两条拉索顶端距离AC为2米,若要使拉索AE与水平桥面的夹角为35°,请计算拉索AE的长.(结果精确到0.1米)(参考数据:sin35°≈![]() ,cos35°≈
,cos35°≈![]() ,tan35°≈
,tan35°≈![]() ,sin72°≈
,sin72°≈![]() ,cos72°≈
,cos72°≈![]() ,tan72°≈
,tan72°≈![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校260名学生参加植树活动,要求每人植4﹣7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵,将各类的人数绘制成扇形图(如图1)和条形图(如图2).
回答下列问题:
(1)补全条形图;
(2)写出这20名学生每人植树量的众数、中位数;
(3)请你计算平均数,并估计这260名学生共植树多少棵?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,匀速行驶.设慢车行驶的时间x(h),两车之的距离为y(km),图中的折线表示y与x之间的函数关系.
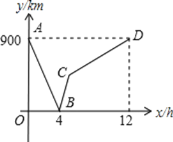
(1)求慢车和快车的速度;
(2)求线段BC所表示的y与x的函数关系式,并写出自变量x的取值范围;
(3)第一列快车出发后又有一列快车(与第一列快车速度相同)从甲地出发,与慢车同时到达各自的目的地.请直接写出第二列快车出发后经过多少小时与慢车相遇,相遇时他们距甲地的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角标系中,已知△ABC三个顶点的坐标分别为A(﹣1,2),B(﹣3,4),C(﹣1,6).
(1)画出△ABC,并求出BC所在直线的解析式;
(2)画出△ABC绕点A顺时针旋转90°后得到的△AB1C1,并求出△ABC在上述旋转过程中扫过的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com