练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    方程的解有多少个？写出其中的几个解来，在直角坐标系中分别描出以这些解为坐标的点，它们在一次函数的图像上吗？在一次函数y＝5－x的图像上任取一点，它的坐标适合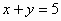方程吗？以方程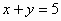的解为坐标的所有点组成的图象与一次函数的图像相同吗？

    答案：
    解析：

    方程的解有无数多个，如：，，，等．

    在直角坐标系中分别描出以这些解为坐标的点，它们都在一次函数的图像上；在一次函数y＝5－x的图像上任取一点，它的坐标一定适合方程；以方程的解为坐标的所有点组成的图象与一次函数的图像完全相同．


    提示：

    以二元一次方程的解为坐标的点都在相应的一次函数图像上，一次函数图像上所有点的坐标都满足相应的二元一次方程．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    九年级（4）班在一次答题活动中，签筒中有4根形状，大小相同的纸签，签里头分别写上了一个方程：①x2-x=0；②（x-1）2-（2x-5）2=0；③x2+12x+36=0；④x2-3x-1=0．
    （1）四个方程中有几个方程有两个相等的实数根并解有关方程；
    （2）小明首先抽签，他看不到纸签上的方程的情况下，从签中随机地抽取一根纸签，那么他抽到两根均为正整数的方程的概率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

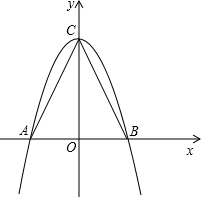    （2012•柳州）如图，在△ABC中，AB=2，AC=BC=
    		5
    ．
    （1）以AB所在的直线为x轴，AB的垂直平分线为y轴，建立直角坐标系如图，请你分别写出A、B、C三点的坐标；
    （2）求过A、B、C三点且以C为顶点的抛物线的解析式；
    （3）若D为抛物线上的一动点，当D点坐标为何值时，S△ABD=
    1
    2
    S△ABC；
    （4）如果将（2）中的抛物线向右平移，且与x轴交于点A′B′，与y轴交于点C′，当平移多少个单位时，点C′同时在以A′B′为直径的圆上（解答过程如果有需要时，请参看阅读材料）．
     
    附：阅读材料
    一元二次方程常用的解法有配方法、公式法和因式分解法，对于一些特殊方程可以通过换元法转化为一元二次方程求解．如解方程：y4-4y2+3=0．
    解：令y2=x（x≥0），则原方程变为x2-4x+3=0，解得x1=1，x2=3．
    当x1=1时，即y2=1，∴y1=1，y2=-1．
    当x2=3，即y2=3，∴y3=
    		3
    ，y4=-
    		3
    ．
    所以，原方程的解是y1=1，y2=-1，y3=
    		3
    ，y4=-
    		3
    ．
    再如x2-2=4
    		x2-2
    ，可设y=
    		x2-2
    ，用同样的方法也可求解．

    查看答案和解析>>

    科目：初中数学 来源：数学教研室 题型：044

    (1)方程x+y=5的解有多少个？写出其中几个？

    (2)在直角坐标系中分别描出以这些解为坐标的点，它们在一次函数y=5－x的图象上吗？

    (3)在一次函数y=5－x的图象上任取一点，它的坐标适合方程x+y=5吗？

    (4)以方程x+y=5的解为坐标的所有点组成的图象与一次函数y=5－x的图象相同吗？

    查看答案和解析>>

    科目：初中数学 来源：2012年广西柳州市中考数学试卷（解析版） 题型：解答题

    如图，在△ABC中，AB=2，AC=BC=．
    （1）以AB所在的直线为x轴，AB的垂直平分线为y轴，建立直角坐标系如图，请你分别写出A、B、C三点的坐标；
    （2）求过A、B、C三点且以C为顶点的抛物线的解析式；
    （3）若D为抛物线上的一动点，当D点坐标为何值时，S△ABD=S△ABC；
    （4）如果将（2）中的抛物线向右平移，且与x轴交于点A′B′，与y轴交于点C′，当平移多少个单位时，点C′同时在以A′B′为直径的圆上（解答过程如果有需要时，请参看阅读材料）．
     
    附：阅读材料
    一元二次方程常用的解法有配方法、公式法和因式分解法，对于一些特殊方程可以通过换元法转化为一元二次方程求解．如解方程：y4-4y2+3=0．
    解：令y2=x（x≥0），则原方程变为x2-4x+3=0，解得x1=1，x2=3．
    当x1=1时，即y2=1，∴y1=1，y2=-1．
    当x2=3，即y2=3，∴y3=，y4=-．
    所以，原方程的解是y1=1，y2=-1，y3=，y4=-．
    再如x2-2=4，可设y=，用同样的方法也可求解．

    查看答案和解析>>

    同步练习册答案