
【题目】如图1,在正方形ABCD中,P为对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F,连接CE.
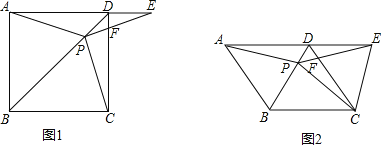
(1)求证:△PCE是等腰直角三角形;
(2)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,判断△PCE的形状,并说明理由.
【答案】(1)见解析;(2)△PCE是等边三角形.理由见解析.
【解析】
(1)由△PDA≌△PDC,推出PA=PC,∠3=∠1,由PA=PE,推出∠2=∠3,推出∠1=∠2,由∠EDF=90°,∠DFE=∠PFC,推出∠FPC=EDF=90°,推出△PEC是等腰直角三角形;
(2)由△PDA≌△PDC,推出PA=PC,∠3=∠1,由PA=PE,推出∠2=∠3,PA═PE=PC,推出∠1=∠2,由∠DFE=∠PFC,推出∠EPC=∠EDC,由∠ADC=120°,推出∠EDC=60°,推出∠EPC=60°,由PE=PC,即可证明△PEC是等边三角形.
(1)证明:如图1中,
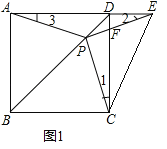
∵四边形ABCD是正方形,
∴AD=DC,∠ADB=∠CDB=45°,∠ADC=90°,
在△PDA和△PDC中,
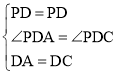 ,
,
∴△PDA≌△PDC,
∴PA=PC,∠3=∠1,
∵PA=PE,
∴∠2=∠3,
∴∠1=∠2,
∵∠EDF=90°,∠DFE=∠PFC,
∴∠FPC=EDF=90°,
∴△PEC是等腰直角三角形.
(2)解:如图2中,结论:△PCE是等边三角形.
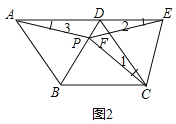
理由:∵四边形ABCD是菱形,
∴AD=DC,∠ADB=∠CDB,∠ADC=∠ABC=120°,
在△PDA和△PDC中,
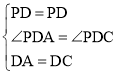 ,
,
∴△PDA≌△PDC,
∴PA=PC,∠3=∠1,
∵PA=PE,
∴∠2=∠3,PA═PE=PC,
∴∠1=∠2,
∵∠DFE=∠PFC,
∴∠EPC=∠EDC,
∵∠ADC=120°,
∴∠EDC=60°,
∴∠EPC=60°,
∵PE=PC,
∴△PEC是等边三角形.


科目:初中数学 来源: 题型:
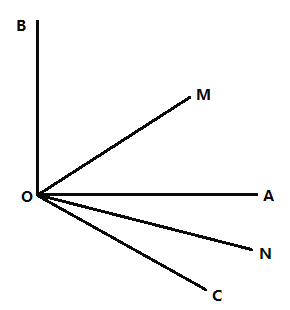
【题目】已知:如图,![]() 是直角,
是直角,![]() 在
在![]() 的外侧,且
的外侧,且![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() 是
是![]() 的平分线.
的平分线.
(1)求![]() 的大小;
的大小;
(2)当锐角![]() 的大小为
的大小为![]() 时,试猜想(1)中
时,试猜想(1)中![]() 的大小是否发生改变?并通过计算说明理由.
的大小是否发生改变?并通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司购买了一批A、B两种型号的产品,其中A型产品的单价比B型产品的单价多6元,已知该公司用1400元购买A型产品的件数与用1160元购买B型产品的件数相等.
(1)求该公司购买的A、B两种型号产品的单价各是多少元?
(2)若两种型号的产品共购买了100件,且购买的总费用为3260元,求购买了多少件A型产品?
查看答案和解析>>
科目:初中数学 来源: 题型:
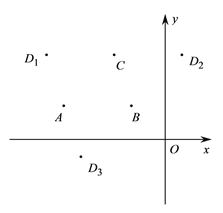
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,以点
,以点![]() 为顶点的平行四边形有三个,记第四个顶点分别为
为顶点的平行四边形有三个,记第四个顶点分别为![]() ,如图所示.
,如图所示.
(1)若![]() ,则点
,则点![]() 的坐标分别是( ),( ),( );
的坐标分别是( ),( ),( );
(2)是否存在点![]() ,使得点
,使得点![]() 在同一条抛物线上?若存在,求出点
在同一条抛物线上?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读理解)若数轴上两点![]() ,
,![]() 所表示的数分别为
所表示的数分别为![]() 和
和![]() ,则有:
,则有:
①![]() ,
,![]() 两点的中点表示的数为
两点的中点表示的数为![]() ;
;
②![]() ,
,![]() 两点之间的距离
两点之间的距离![]() ;若
;若![]() ,则可简化为
,则可简化为![]() .
.
(解决问题)数轴上两点![]() ,
,![]() 所表示的数分别为
所表示的数分别为![]() 和
和![]() ,且满足
,且满足![]() .
.
(1)求出![]() ,
,![]() 两点的中点
两点的中点![]() 表示的数;
表示的数;
(2)点![]() 从原点
从原点![]() 点出发向右运动,经过
点出发向右运动,经过![]() 秒后点
秒后点![]() 到
到![]() 点的距离是点
点的距离是点![]() 到
到![]() 点距离的
点距离的![]() 倍,求点
倍,求点![]() 的运动速度是每秒多少个单位长度?
的运动速度是每秒多少个单位长度?
(数学思考)
(3)点![]() 以每秒
以每秒![]() 个单位的速度从原点
个单位的速度从原点![]() 出发向右运动,同时,点
出发向右运动,同时,点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 个单位的速度向左运动,点
个单位的速度向左运动,点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度向右运动,
个单位的速度向右运动,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.思考:在运动过程中,
的中点.思考:在运动过程中,![]() 的值是否发生变化?如果没有变化,请求出这个值;如果发生变化,请说明理由.
的值是否发生变化?如果没有变化,请求出这个值;如果发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年小张前五个月的奖金变化情况如下表(正数表示比前一月多的钱数,负数表示比前一月少的钱数,单位:元)
月份 | 一月 | 二月 | 三月 | 四月 | 五月 |
钱数变化 |
|
|
|
|
|
若2018年12月份小张的奖金为![]() 元.
元.
(1)用代数式表示2019年二月份小张的奖金为___________元;
(2)小张五月份所得奖金比二月份多多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察算式:1×3+1=4=22;2×4+1=9=32;3×5+1=16=42;4×6+1=25=52,…
(1)请根据你发现的规律填空:6×8+1=( )2;
(2)用含n的等式表示上面的规律: ;
(3)用找到的规律解决下面的问题:
计算:(1+![]() )(1+
)(1+![]() )(1+
)(1+![]() )(1+
)(1+![]() )…(1+
)…(1+![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会为积极响应武汉市文明创建活动,组织有关方面的知识竞赛,共设有20道选择题,各题分值相同,每题必答,下表记录了3个参赛者的得分情况.
参赛者 | 答对题数 | 答错题数 | 得分 |
A | 20 | 0 | 100 |
B | 19 | 1 | 94 |
C | 18 | 2 | 88 |
(1)设答对一题记a分,答错一题记b分,则a= b= ;
(2)参赛者E说他得了80分,你认为可能吗,为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com