
如图1,梯形 中,
中, ∥
∥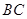 ,
, ,
, .一个动点
.一个动点 从点
从点 出发,以每秒
出发,以每秒 个单位长度的速度沿线段
个单位长度的速度沿线段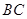 方向运动,过点
方向运动,过点 作
作 ,交折线段
,交折线段 于点
于点 ,以
,以 为边向右作正方形
为边向右作正方形 ,点
,点 在射线
在射线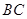 上,当
上,当 点到达
点到达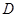 点时,运动结束.设点
点时,运动结束.设点 的运动时间为
的运动时间为 秒(
秒( ).
).
(1)当正方形 的边
的边 恰好经过点
恰好经过点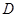 时,求运动时间
时,求运动时间 的值;
的值;
(2)在整个运动过程中,设正方形 与△
与△ 的重合部分面积为
的重合部分面积为 ,请直接写出
,请直接写出 与
与 之间的函数关系式和相应的自变量
之间的函数关系式和相应的自变量 的取值范围;
的取值范围;
(3)如图2,当点 在线段
在线段 上运动时,线段
上运动时,线段 与对角线
与对角线 交于点
交于点 ,将△
,将△ 沿
沿 翻折,得到△
翻折,得到△ ,连接
,连接 .是否存在这样的
.是否存在这样的 ,使△
,使△ 是等腰三角形?若存在,求出对应的
是等腰三角形?若存在,求出对应的 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

(1)当t=4时,正方形PQMN的边MN恰好过点D
(2)
(3)当 时,∆PEF是等腰三角形
时,∆PEF是等腰三角形
解析试题分析:(1)作AG⊥BC,DH⊥BC,垂足分别为G、H,可以得出四边形AGHD为矩形,根据矩形的性质及相关条件可以得出△ABG≌△DCH,可以求出BG=CH的值,再由勾股定理就可以求出AG=DH的值,就可以求出BP的值,即可以求出结论t的值;
(2)运用求分段函数的方法,分四种情况,当0<t≤3,当3<t≤4,4<t≤7,7<t≤8时,运用梯形的面积公式和三角形的面积公式就可以求出S的值;
(3)先由条件可以求出EF=EQ=PQ-EP=4- t,分为三种情况:EF=EP时可以求出t值,当FE=FP时,作FR⊥EP,垂足为R,可以求出t值,当PE=PF时,作PS⊥EF,垂足为S,可以求出t值.
t,分为三种情况:EF=EP时可以求出t值,当FE=FP时,作FR⊥EP,垂足为R,可以求出t值,当PE=PF时,作PS⊥EF,垂足为S,可以求出t值.
试题解析:(1)如图2,作AG⊥BC于G,DH⊥BC于H,则四边形AGHD是矩形。
∵梯形ABCD中,AB=AD=DC=5,
∴∆ABG≌∆DCH,
∴ ,
,
∴当正方形PQMN的边MN恰好过点D时,点M与点D重合,此时MQ=4, ,
,
∴当t=4时,正方形PQMN的边MN恰好过点D。
(2)
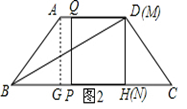

如图1,当0<t≤3时,BP=t,∵
∴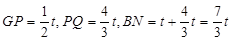 ,
,
如图3,当3<t≤4时,BP="t," 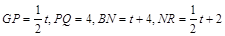
∴


如图4,当4<t≤7时,BP="t," 
∴
如图5,当7<t≤8时,BP="t," 
∴
∴
(3)∵ ,
,
∴
∴
由(1)可知 则
则



如图6,当EF=EP时,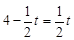
∴
如图7,当FE=FP时,作FR⊥EP于R,∴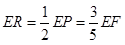
∴
∴
如图8,当PE=PF时,作PS⊥EF于S,∴
∴
∴
∴当 时,∆PEF是等腰三角形。
时,∆PEF是等腰三角形。
考点:相似形综合题.


科目:初中数学 来源: 题型:解答题
(1)如图1,Rt△ABC中,∠B=90°,AB=2BC,现以C为圆心、CB长为半径画弧交边AC于D,再以A为圆心、AD为半径画弧交边AB于E.求证: .(这个比值
.(这个比值
叫做AE与AB的黄金比.)
(2)如果一等腰三角形的底边与腰的比等于黄金比,那么这个等腰三角形就叫做黄金三角形.请你以图2中的线段AB为腰,用直尺和圆规,作一个黄金三角形ABC.
(注:直尺没有刻度!作图不要求写作法,但要求保留作图痕迹,并对作图中涉及到的点用字母进行标注)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,矩形ABCD为台球桌面,AD=260cm,AB=130cm,球目前在E点位置,AE=60cm.如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.
(1)求证:△BEF∽△CDF;
(2)求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在数学课上,同学们研究图形的拼接问题.
比如:两个全等的等腰直角三角形纸片既能拼成一个大的等腰直角三角形(如图1),也能拼成一个正方形(如图2).
(1)现有两个相似的直角三角形纸片,各有一个角为 ,恰好可以拼成另一个含有30°角的直角三角形,那么在原来的两个三角形纸片中,较大的与较小的纸片的相似比为________,请画出拼接的示意图;
,恰好可以拼成另一个含有30°角的直角三角形,那么在原来的两个三角形纸片中,较大的与较小的纸片的相似比为________,请画出拼接的示意图;
(2)现有一个矩形恰好由三个各有一个角为 的直角三角形纸片拼成,请你画出两种不同拼法的示意图.在拼成这个矩形的三角形中,若每种拼法中最小的三角形的斜边长为
的直角三角形纸片拼成,请你画出两种不同拼法的示意图.在拼成这个矩形的三角形中,若每种拼法中最小的三角形的斜边长为 ,请直接写出每种拼法中最大三角形的斜边长.
,请直接写出每种拼法中最大三角形的斜边长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:如图,在△ABC中,点D是BC中点,点E是AC中点,且AD⊥BC,BE⊥AC, BE,AD相交于点G,过点B作BF∥AC交AD的延长线于点F, DF="6."
(1) 求AE的长;
(2) 求 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
阅读下面的材料:
小明遇到一个问题:如图(1),在□ABCD中,点E是边BC的中点,点F是线段AE上一点,BF的延长线交射线CD于点G.如果 ,求
,求 的值.
的值. 
他的做法是:过点E作EH∥AB交BG于点H,则可以得到△BAF∽△HEF.
请你回答:(1)AB和EH的数量关系为 ,CG和EH的数量关系为 , 的值为 .
的值为 .
(2)如图(2),在原题的其他条件不变的情况下,如果 ,那么
,那么 的值为 (用含a的代数式表示).
的值为 (用含a的代数式表示).
(3)请你参考小明的方法继续探究:如图(3),在四边形ABCD中,DC∥AB,点E是BC延长线上一点,AE和BD相交于点F. 如果 ,那么
,那么 的值为 (用含m,n的代数式表示).
的值为 (用含m,n的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com