
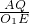 ��ֵ���䣻��AQ•O1E��ֵ���䣬��������ֻ��һ��������ȷ������ѡ����ȷ�Ľ���֤������ֵ��
��ֵ���䣻��AQ•O1E��ֵ���䣬��������ֻ��һ��������ȷ������ѡ����ȷ�Ľ���֤������ֵ��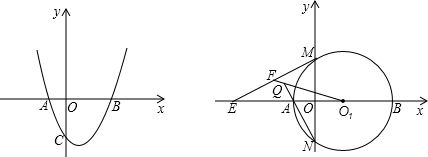
 =1��
=1�� =
= ��
�� ����N��0��-
����N��0��- ����
���� ����
����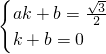 ��
��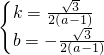 ��
��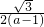 x-
x-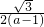 �٣�
�٣� ��0����
��0���� x-
x- �ڣ�
�ڣ�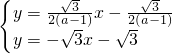 ��
��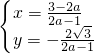 ��
��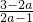 ��-
��- ����
����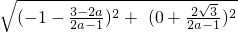 =|
=|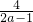 |��
|��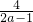 |•��1-2a��=4��ֵ���䣮
|•��1-2a��=4��ֵ���䣮


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
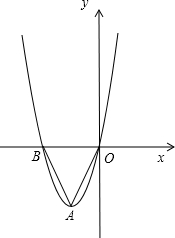 ��ͼ��������y=x2+4x��x��ֱ��ཻ�ڵ�B��O�����Ķ���ΪA������AB��AO��
��ͼ��������y=x2+4x��x��ֱ��ཻ�ڵ�B��O�����Ķ���ΪA������AB��AO���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 16����ͼ��������y=-x2+2x+m��m��0����x���ཻ�ڵ�A��x1��0����B��x2��0������A�ڵ�B����࣮��x=x2-2ʱ��y
16����ͼ��������y=-x2+2x+m��m��0����x���ཻ�ڵ�A��x1��0����B��x2��0������A�ڵ�B����࣮��x=x2-2ʱ��y�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��֪��ͼ��������y=x2+��k2+1��x+k+1�ĶԳ�����ֱ��x=-1���Ҷ�����x���Ϸ�����M��ֱ��x=-1����������ϵ�һ���㣬����M��x��Ĵ���MG������ΪG������M��ֱ��x=-1�Ĵ���MN������ΪN��ֱ��x=-1��x��Ľ���H�㣬��M��ĺ�����Ϊx������MNHG���ܳ�Ϊl��
��֪��ͼ��������y=x2+��k2+1��x+k+1�ĶԳ�����ֱ��x=-1���Ҷ�����x���Ϸ�����M��ֱ��x=-1����������ϵ�һ���㣬����M��x��Ĵ���MG������ΪG������M��ֱ��x=-1�Ĵ���MN������ΪN��ֱ��x=-1��x��Ľ���H�㣬��M��ĺ�����Ϊx������MNHG���ܳ�Ϊl���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��2013•���ݣ���ͼ��������y=x2-2x-8��y���ڵ�A����x���������ڵ�B��
��2013•���ݣ���ͼ��������y=x2-2x-8��y���ڵ�A����x���������ڵ�B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
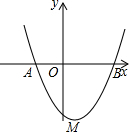 ��ͼ��������y=x2-2x-3��x��ֱ���A��B���㣮
��ͼ��������y=x2-2x-3��x��ֱ���A��B���㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com