
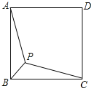
【题目】如图,点![]() 是正方形
是正方形![]() 内一点,连接
内一点,连接![]() 、
、![]() 、
、![]() ,若
,若![]() ,
,![]() ,
,![]() ,则正方形
,则正方形![]() 的边长为________.
的边长为________.
【答案】![]()
【解析】
将△ABP绕点B沿顺时针方向旋转90°到△BCQ的位置,连接PQ;先求出PQ的长,再求出∠PQC=90°,利用勾股定理求出QC的长,最后利用勾股定理求出BC的长.
如图,将△ABP绕点B沿顺时针方向旋转90°,
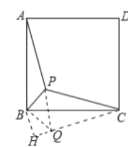
到△BCQ的位置,连接PQ;
则BQ=BP=![]() ,∠BQC=∠BPA=135°,
,∠BQC=∠BPA=135°,
则△PBQ是等腰直角三角形,
即PQ=![]() ,
,
故∠BQP=∠BPQ=45°,∠PQC=135°45°=90°;
由勾股定理得:QC2=PC2PQ2,,CQ=2![]() 在△BQC中,∠BQC=135°,BQ=
在△BQC中,∠BQC=135°,BQ=![]() ,CQ=2
,CQ=2![]() ,
,
过B作BH垂直CQ,交CQ的延长线于H;则CH=CQ+QH,BH=HQ=![]() ,
,
解得:BC2=BH2+CH2,BC=![]()
故答案为![]() .
.


科目:初中数学 来源: 题型:
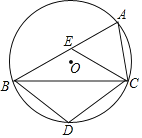
【题目】如图,△ABC是⊙O的内接三角形,点D在![]() 上,点E在弦AB上(E不与A重合),且四边形BDCE为菱形.
上,点E在弦AB上(E不与A重合),且四边形BDCE为菱形.
(1)求证:AC=CE;
(2)求证:BC2﹣AC2=ABAC;
(3)已知⊙O的半径为3.
①若![]() =
=![]() ,求BC的长;
,求BC的长;
②当![]() 为何值时,ABAC的值最大?
为何值时,ABAC的值最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
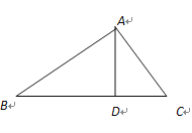
【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.
(1)求作∠ABC的平分线,分别交AD,AC于E,F两点;(要求:尺规作图,保留作图痕迹,不写作法)
(2)证明:AE=AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC中,AB=AC=BC=10厘米,M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度是1厘米/秒的速度,点N的速度是2厘米/秒,当点N第一次到达B点时,M、N同时停止运动.
(1)M、N同时运动几秒后,M、N两点重合?
(2)M、N同时运动几秒后,可得等边三角形△AMN?
(3)M、N在BC边上运动时,能否得到以MN为底边的等腰△AMN,如果存在,请求出此时M、N运动的时间?

查看答案和解析>>
科目:初中数学 来源: 题型:
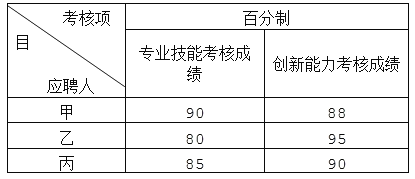
【题目】某广告公司为了招聘一名创意策划,准备从专业技能和创新能力两方面进行考核,成绩高者录取.甲、乙、丙三名应聘者的考核成绩以百分制统计如下:
(1)如果公司认为专业技能和创新能力同等重要,则应聘人 将被录取.
(2)如果公司认为职员的创新能力比专业技能重要,因此分别赋予它们6和4的权.计算他们赋权后各自的平均成绩,并说明谁将被录取.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一次函数![]() (
(![]() 为常数)的图像位于
为常数)的图像位于![]() 轴下方的部分沿
轴下方的部分沿![]() 轴翻折到
轴翻折到![]() 轴上方,和一次函数
轴上方,和一次函数![]() (
(![]() 为常数)的图像位于
为常数)的图像位于![]() 轴及上方的部分组成“
轴及上方的部分组成“![]() ”型折线,过点
”型折线,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() ,若该“
,若该“![]() ”型折线在直线
”型折线在直线![]() 下方的点的横坐标
下方的点的横坐标![]() 满足
满足![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
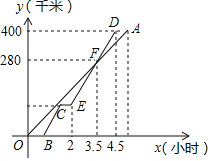
【题目】慢车和快车先后从甲地出发沿直线道路匀速驶向乙地,快车比慢车晚出发0.5小时,行驶一段时间后,快车途中休息,休息后继续按原速行驶,到达乙地后停止.慢车和快车离甲地的距离y(千米)与慢车行驶时间x(小时)之间的函数关系如图所示.有以下说法:①快车速度是120千米/小时;②慢车到达乙地比快车到达乙地晚了0.5小时;③点C坐标(![]() ,100);④线段BC对应的函数表达式为y=120x﹣60(0.5≤x≤
,100);④线段BC对应的函数表达式为y=120x﹣60(0.5≤x≤![]() );其中正确的个数有( )
);其中正确的个数有( )
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com