
【题目】某地城管需要从甲、乙两个仓库向A、B两地分别运送10吨和5吨的防寒物资,甲、乙两仓库分别有8吨、7吨防寒物资.从甲、乙两仓库运送防寒物资到A、B两地的运费单价(元/吨)如表1,设从甲仓库运送到A地的防寒物资为x吨(如表2).
表1
甲仓库 | 乙仓库 | |
A地 | 80 | 100 |
B地 | 60 | 40 |
表2
甲仓库 | 乙仓库 | |
A地 | 10-x | |
B地 |
(1)完成表2;
(2)求运送的总运费y(元)与x(吨)之间的函数表达式,并直接写出x的取值范围;
(3)求最低总运费.
【答案】(1)8-x x-3 (2)![]() (
(![]() ) (3)1040元
) (3)1040元
【解析】
(1)由题意填表即可;.
(2)根据题意表示出甲仓库和乙仓库分别运往A、B两地的物资数,再由等量关系:总运费=甲仓库运往A地的费用+甲仓库运往B地的费用+乙仓库运往A地的费用+乙仓库运往B地的费用列式并化简解答即可;.
(3)因为所得的函数为一次函数,由增减性可知:y随x增大而减少,则当x=8时,y最小,并求出最小值即可.
(1)设从甲仓库运送到A地的防寒物资为x吨,可得从甲仓库运送到B地的防寒物资为8-x吨,从乙仓库运送到B地的防寒物资为x-3吨;.
故答案为:8-x、x-3;
(2)![]() ,
,
化简得![]() .
.
其中![]() .
.
(3)由(2)得![]() ,y随x增大而减少,
,y随x增大而减少,
所以当x=8时总运费最小,
当x=8时,![]() .
.
最低总运费为1040元.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知矩形OABC的三个顶点A(0,10),B(8,10),C(8,0),过O、C两点的抛物线y=ax2+bx+c与线段AB交于点D,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.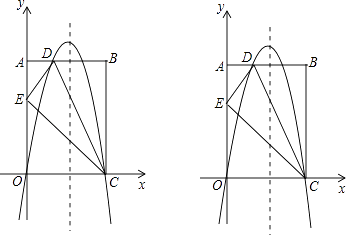
(1)求AD的长及抛物线的解析式;
(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动.设运动时间为t秒.请问当t为何值时,以P、Q、C为顶点的三角形是等腰三角形?
(3)若点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M、N、C、E为顶点四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,AB=AC,点D为BC中点.∠MDN=900,∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.下列结论
①(BE+CF)=![]() BC,②
BC,②![]() ,③
,③![]() AD·EF,④AD≥EF,⑤AD与EF可能互相平分,
AD·EF,④AD≥EF,⑤AD与EF可能互相平分,
其中正确结论的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,点D,E分别在AC,BC上,且AD=CE,AE与BD相交于点P,BF⊥AE于点F.若PF=2,则BP=( )

A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]() ;
;
(2)![]() ;
;
(3)先化简,再求值![]() ,其中
,其中![]() ,
,![]() ;
;
(4)长方形和正方形按如图的样式摆放,求图中阴影部分的面积;

(5)用乘法公式计算: ![]() ;
;
(6)已知![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场投入13 800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
类别/单价 | 成本价 | 销售价(元/箱) |
甲 | 24 | 36 |
乙 | 33 | 48 |
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在校园文化建设中,某学校原计划按每班5幅订购了“名人字画”共90幅.由于新学期班数增加,决定从阅览室中取若干幅“名人字画”一起分发,如果每班分4幅,则剩下17幅;如果每班分5幅,则最后一班不足3幅,但不少于1幅.
(1)该校原有的班数是多少个?
(2)新学期所增加的班数是多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】细心观察图,认真分析各式,然后解答问题:
![]() ;
;
![]() ;
;
![]() ;
;![]()

(1)请用含![]() (
(![]() 为正整数)的等式表示上述交化规律:______;
为正整数)的等式表示上述交化规律:______;
(2)观察总结得出结论:直角三角形两条直角边与斜边的关系,用一句话概括为:______;
(3)利用上面的结论及规律,请在图中作出等于![]() 的长度;
的长度;
(4)若![]() 表示三角形面积,
表示三角形面积,![]() ,
,![]() ,
,![]()
![]() ,计算出
,计算出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com