
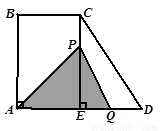
如图,梯形ABCD中,AD∥BC,∠BAD=90°,CE⊥AD于点E,AD=4cm,BC=2cm,AB=3cm.从初始时刻开始,动点P、Q 分别从点A、B同时出发,运动速度均为1 cm/s,动点P沿A→B→C→E的方向运动,到点E停止;动点Q沿B→C→E→D的方向运动,到点D停止.设运动时间为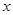 s,
s,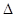 PAQ的面积为y cm2.(这里规定:线段是面积为0的三角形)解答下列问题:
PAQ的面积为y cm2.(这里规定:线段是面积为0的三角形)解答下列问题:

(1)当x= 2 s时,y=________cm2;当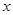 =
= 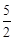 s时,y=________cm2;
s时,y=________cm2;
(2)当动点P在线段BC上运动,即3 ≤ x ≤ 5时,求y与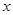 之间的函数关系式,并求出
之间的函数关系式,并求出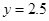 时
时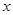 的值;
的值;
(3)当动点P在线段CE上运动,即5 < x ≤ 8 时,求y与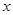 之间的函数关系式;
之间的函数关系式;
(4)直接写出在整个运动过程中,使PQ与四边形ABCE的对角线平行的所有x的值.
(1)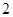 ;
;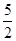 (2)y
(2)y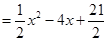 ,4(3)y
,4(3)y 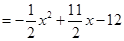 ,y
,y (4)
(4) ;
;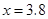 ;
;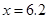 .
.
【解析】解:(1)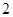 ;
;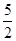 .························ (2分)
.························ (2分)
(2)当3≤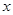 ≤5时,
≤5时,
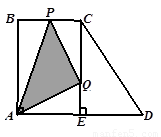
 ······················· (3分)
······················· (3分)
 ············ (4分)
············ (4分)
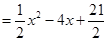 .···························· (5分)
.···························· (5分)
当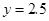 时,
时,
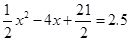 ·························· (6分)
·························· (6分)
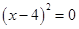
解得 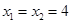
∴当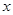 =4时,
=4时,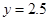 .·························· (7分)
.·························· (7分)
(3)当5<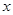 ≤7时,
≤7时,
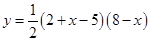 ························· (8分)
························· (8分)
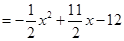 .·························· (9分)
.·························· (9分)
当7<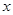 ≤8时,
≤8时,
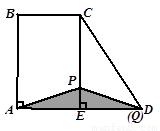
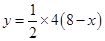 ···························· (10分)
···························· (10分)
 .······························ (11分)
.······························ (11分)
(4) ;
;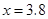 ;
;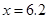 . (14分)
. (14分)
本试题主要是考查了动点运用的轨迹问题。通过已知的边长和运动的速度可以分析,经过一丁点时候后,两点的距离,以及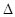 PAQ的面积为y
cm2,同时在不同的时刻,面积表示不同。
PAQ的面积为y
cm2,同时在不同的时刻,面积表示不同。
(1)当x=2时,则AP=2,BQ=2,如图所示,则面积可以利用底乘以高的一半得到。
(2)当点P在线段BC上运动,即3 ≤ x ≤ 5时,同样可知得到三角形的面积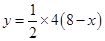 ,然后代值得到当y=2时的对应x的值。
,然后代值得到当y=2时的对应x的值。
(3)利用动点P在线段CE上运动,即5 < x ≤ 8 时,同上分析三角形的边的关系,利用面积公式求解得到。
(4)根据在整个运动过程中,使PQ与四边形ABCE的对角线平行,那么利用平行关系,得到所有x的值.


科目:初中数学 来源: 题型:
 如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2,cosC=
如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2,cosC=
| ||
| 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com