
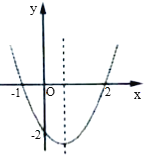
【题目】二次函数![]() 的图象如图所示,以下结论:①
的图象如图所示,以下结论:①![]() ;②顶点坐标为
;②顶点坐标为![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .正确的有_______.(填序号)
.正确的有_______.(填序号)
【答案】①⑤
【解析】
根据图象的开口方向可知a>0,根据抛物线与x轴的交点可得对称轴方程,根据抛物线与y轴的交点可得c<0,根据对称轴方程即可确定b的符号,即可对①②③进行判断,根据二次函数的增减性即可对④进行判断,根据点(-1,0)是图象与x轴的交点可对⑤进行判断,综上即可得答案.
∵图象的开口向上,
∴a>0,
∵图象与x轴的交点为(-1,0)和(2,0),
∴对称轴方程为x=![]() =
=![]() =
=![]() >0,
>0,
∴b<0,
∵图象与y轴交于y轴负半轴,
∴c<0,
∴abc>0,故①正确,
∵对称轴为x=![]() ,图象与y轴交于(0,-2),
,图象与y轴交于(0,-2),
∴抛物线顶点坐标不是(![]() ,-2),故②错误,
,-2),故②错误,
∵![]() =
=![]() ,
,
∴a+b=0,故③错误,
当x=1时,a+b+c<0,故④错误,
当x=-1时,a-b+c=0,故⑤正确,
综上所述:正确的结论有①⑤,
故答案为:①⑤


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
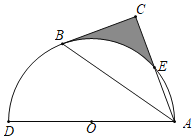
【题目】如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E;B、E是半圆弧的三等分点,![]() 的长为
的长为![]() ,则图中阴影部分的面积为( )
,则图中阴影部分的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解并解决问题:一般地,如果把一个图形绕着一个定点旋转一定角度![]() (
(![]() 小于
小于![]() )后,能够与原来的图形重合,那么这个图形叫做旋转对称图形,这个定点叫做旋转对称中心.
)后,能够与原来的图形重合,那么这个图形叫做旋转对称图形,这个定点叫做旋转对称中心.![]() 叫做这个旋转对称图形的一个旋转角.请依据上述定义解答下列问题:
叫做这个旋转对称图形的一个旋转角.请依据上述定义解答下列问题:
(1)请写出一个旋转对称图形,这个图形有一个旋转角是![]() .这个图形可以是______;
.这个图形可以是______;
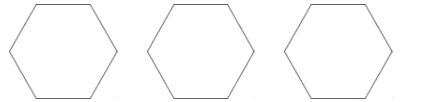
(2)为了美化环境,某中学需要在一块正六边形空地上分别种植六种不同的花草,现将这块空地按下列要求分成六块:①分割后的整个图形必须既是轴对称图形又是旋转对称图形;②六块图形的面积相同.请你按上述两个要求,分别在图中的三个正六边形中画出三种不同的分割方法(只要求画图正确,不写作法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,其中
两点,其中![]() ,
,![]() .该抛物线与
.该抛物线与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于另一点
轴交于另一点![]() .
.

(1)求![]() 的值及该抛物线的解析式;
的值及该抛物线的解析式;
(2)如图2.若点![]() 为线段
为线段![]() 上的一动点(不与
上的一动点(不与![]() 重合).分别以
重合).分别以![]() 、
、![]() 为斜边,在直线
为斜边,在直线![]() 的同侧作等腰直角△
的同侧作等腰直角△![]() 和等腰直角△
和等腰直角△![]() ,连接
,连接![]() ,试确定△
,试确定△![]() 面积最大时
面积最大时![]() 点的坐标.
点的坐标.
(3)如图3.连接![]() 、
、![]() ,在线段
,在线段![]() 上是否存在点
上是否存在点![]() ,使得以
,使得以![]() 为顶点的三角形与△
为顶点的三角形与△![]() 相似,若存在,请直接写出点
相似,若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】罚球是篮球比赛中得分的一个组成部分,罚球命中率的高低对篮球比赛的结果影响很大.如图是对某球员罚球训练时命中情况的统计:
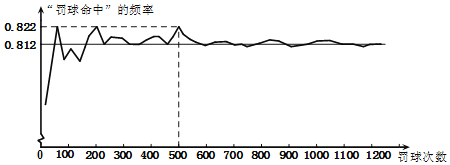
下面三个推断:①当罚球次数是500时,该球员命中次数是411,所以“罚球命中”的概率是0.822;②随着罚球次数的增加,“罚球命中”的频率总在0.812附近摆动,显示出一定的稳定性,可以估计该球员“罚球命中”的概率是0.812;③由于该球员“罚球命中”的频率的平均值是0.809,所以“罚球命中”的概率是0.809.其中合理的是( )
A.①B.②C.①③D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x+b的图象与x轴、y轴分别交于A,B两点,与反比例函数y=![]() 的图象分别交于C,D两点,点C(2,4),点B是线段AC的中点.
的图象分别交于C,D两点,点C(2,4),点B是线段AC的中点.
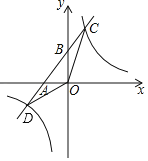
(1)求一次函数y=k1x+b与反比例函数y=![]() 的解析式;
的解析式;
(2)求△COD的面积;
(3)直接写出当x取什么值时,k1x+b<![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com