
【题目】如图,在平面直角坐标系中,正比例函数![]() 与反比例函数
与反比例函数![]() 的图象分别交于
的图象分别交于![]() ,
,![]() 两点,已知点
两点,已知点![]() 与点
与点![]() 关于坐标原点
关于坐标原点![]() 成中心对称,且点
成中心对称,且点![]() 的坐标为
的坐标为![]() .其中
.其中![]() .
.
(1)四边形![]() 是 .(填写四边形
是 .(填写四边形![]() 的形状)
的形状)
(2)当点![]() 的坐标为
的坐标为![]() 时,且四边形
时,且四边形![]() 是矩形,求
是矩形,求![]() ,
,![]() 的值.
的值.
(3)试探究:随着![]() 与
与![]() 的变化,四边形
的变化,四边形![]() 能不能成为菱形?若能,请直接写出
能不能成为菱形?若能,请直接写出![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.

【答案】(1) 平行四边形;(2)![]() ;(3) 四边形
;(3) 四边形 ![]() 不可能成为菱形,理由见解析.
不可能成为菱形,理由见解析.
【解析】(1)根据正、反比例函数的对称性即可得出点A、C关于原点O成中心对称,再结合点B与点D关于坐标原点O成中心对称,即可得出对角线BD、AC互相平分,由此即可证出四边形ABCD的是平行四边形;
(2)由点A的纵坐标结合反比例函数图象上点的坐标特征即可求出n值,进而得出点A的坐标以及OA的长度,再根据矩形的性质即可得出OB=OA,由点B的坐标即可求出m值;
(3)由点A在第一象限内,点B在x轴正半轴上,可得出∠AOB<90°,而菱形的对角线互相垂直平分,由此即可得知四边形ABCD不可能成为菱形.
(1)∵正比例函数y=kx(k>0)与反比例函数y=![]() 的图象分别交于A、C两点,
的图象分别交于A、C两点,
∴点A、C关于原点O成中心对称,
∵点B与点D关于坐标原点O成中心对称,
∴对角线BD、AC互相平分,
∴四边形ABCD的是平行四边形.
故答案为:平行四边形.
(2)∵点A(n,3)在反比例函数y=![]() 的图象上,
的图象上,
∴3n=3,解得:n=1,
∴点A(1,3),
∴OA=![]() .
.
∵四边形ABCD为矩形,
∴OA=![]() AC,OB=
AC,OB=![]() BD,AC=BD,
BD,AC=BD,
∴OB=OA=![]() ,
,
∴m=![]() .
.
(3)四边形ABCD不可能成为菱形,理由如下:
∵点A在第一象限内,点B在x轴正半轴上,
∴∠AOB<90°,
∴AC与BD不可能互相垂直,
∴四边形ABCD不可能成为菱形.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】列方程解应用题.
程大位,明代商人,珠算发明家,被称为珠算之父、卷尺之父.少年时,读书极为广博,对数学颇感兴趣,60岁时完成其杰作《直指算法统宗》(简称《算法统宗》).
在《算法统宗》里记载了一道趣题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完.试问大、小和尚各多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一张长方形纸片ABCD,已知AB=8,AD=7,E为AB上一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在长方形ABCD的某一条边上,则等腰三角形AEP的底边长是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设抛物线的解析式为y=ax2 , 过点B1(1,0)作x轴的垂线,交抛物线于点A1(1,2);过点B2( ![]() ,0)作x轴的垂线,交抛物线于点A2;…;过点Bn((
,0)作x轴的垂线,交抛物线于点A2;…;过点Bn(( ![]() )n﹣1 , 0)(n为正整数)作x轴的垂线,交抛物线于点An , 连接AnBn+1 , 得Rt△AnBnBn+1 .
)n﹣1 , 0)(n为正整数)作x轴的垂线,交抛物线于点An , 连接AnBn+1 , 得Rt△AnBnBn+1 .
(1)求a的值;
(2)直接写出线段AnBn , BnBn+1的长(用含n的式子表示);
(3)在系列Rt△AnBnBn+1中,探究下列问题:
①当n为何值时,Rt△AnBnBn+1是等腰直角三角形?
②设1≤k<m≤n(k,m均为正整数),问:是否存在Rt△AkBkBk+1与Rt△AmBmBm+1相似?若存在,求出其相似比;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=2,FD=4,则BC的长为( ) 
A.6 ![]()
B.2 ![]()
C.4 ![]()
D.4 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
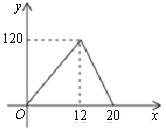
【题目】李刚家去年养殖的“丰收一号”多宝鱼喜获丰收,上市20天全部售完,李刚对销售情况进行了跟踪记录,并将记录情况绘成图象,日销售量y(单位:千克)与上市时间x(单位:天)的函数关系如图所示.
(1)观察图象,直接写出日销售量的最大值;
(2)求李刚家多宝鱼的日销售量y与上市时间x的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知凸四边形ABCD中,∠A=∠C=90°.


(1)如图1,若DE平分∠ADC,BF平分∠ABC的邻补角,判断DE与BF位置关系并证明.
(2)如图2,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE与BF位置关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() 点P从A点出发沿
点P从A点出发沿![]() 路径向终点运动,终点为B点;点Q从B点出发沿
路径向终点运动,终点为B点;点Q从B点出发沿![]() 路径向终点运动,终点为A点
路径向终点运动,终点为A点![]() 点P和Q分别以1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作
点P和Q分别以1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作![]() 于E,
于E,![]() 于
于![]() 问:点P运动多少时间时,
问:点P运动多少时间时,![]() 与QFC全等?请说明理由.
与QFC全等?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数.
小明的解题思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠APC=50°+60°=110°.
问题迁移:
(1)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.试判断∠CPD、∠α、∠β之间有何数量关系?请说明理由;


(2)在(1)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com