
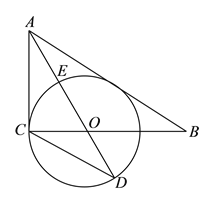
【题目】如图,在![]() 中,
中, ![]() ,
, ![]() 是
是![]() 的角平分线,以
的角平分线,以![]() 为圆心,
为圆心, ![]() 为半径作⊙
为半径作⊙![]() .
.
(![]() )求证:
)求证: ![]() 是⊙
是⊙![]() 的切线.
的切线.
(![]() )已知
)已知![]() 交⊙
交⊙![]() 于点
于点![]() ,延长
,延长![]() 交⊙
交⊙![]() 于点
于点![]() ,
, ![]() ,求
,求![]() 的值.
的值.
(![]() )在(
)在(![]() )的条件下,设⊙
)的条件下,设⊙![]() 的半径为
的半径为![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:对于(1),过O作OF⊥AB于F,由角平分线上的点到角两边的距离相等即可得证;
对于(2),连接CE,结合角平分线的性质和弦切角定理可证明△ACE∽△ADC,可得![]() =tanD,即可解答;
=tanD,即可解答;
对于(3),先由勾股定理求得AE的长,再证明△BOF∽△BAC,得![]() ,设BO=y,BF=z,列二元一次方程组即可解决问题.
,设BO=y,BF=z,列二元一次方程组即可解决问题.
试题解析:( ![]() )证明:作
)证明:作![]() 于
于![]() ,
,
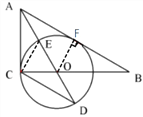
∵![]() 是
是![]() 的角平分线,
的角平分线, ![]() ,
,
∴![]() ,
,
∴![]() 是⊙
是⊙![]() 的切线.
的切线.
(![]() )连接
)连接![]() ,
,
∵![]() 是
是![]() 的角平分线,
的角平分线,
∴![]() ,
,
∵![]() 所对的弧于
所对的弧于![]() 所对的弧是同弧,
所对的弧是同弧,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(![]() )设
)设![]() ,在
,在![]() 中,
中,
由勾股定理得![]() ,解得
,解得![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
设![]() ,
, ![]() ,
,
则![]() ,
,
即![]() ,
,
![]() ,
,
解得![]() ,
, ![]() .
.
∴![]() .
.


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】我们知道对于x轴上的任意两点A(x1,0),B(x2,0),有AB=|x1﹣x2|,而对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1﹣x2|+|y1﹣y2|称为Pl,P2两点间的直角距离,记作d(P1,P2),即d(P1,P2)=|x1﹣x2|+|y1﹣y2|.
(1)已知O为坐标原点,若点P坐标为(1,3),则d(O,P)= ;
(2)已知O为坐标原点,动点P(x,y)满足d(O,P)=2,请写出x与y之间满足的关系式,并在所给的直角坐标系中画出所有符合条件的点P所组成的图形;
(3)试求点M(2,3)到直线y=x+2的最小直角距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
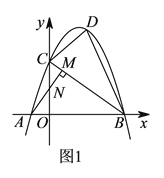
【题目】如图1,在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,点
,点![]() 为
为![]() 轴负半轴上一点,
轴负半轴上一点, ![]() 于点
于点![]() 交
交![]() 轴于点
轴于点![]() .已知抛物线
.已知抛物线![]() 经过点
经过点![]() 、
、![]() 、
、![]() .
.
(![]() )求抛物线的函数式.
)求抛物线的函数式.
(![]() )连接
)连接![]() ,点
,点![]() 在线段
在线段![]() 上方的抛物线上,连接
上方的抛物线上,连接![]() 、
、![]() ,若
,若![]() 和
和![]() 面积满足
面积满足![]() ,求点
,求点![]() 的坐标.
的坐标.
(![]() )如图
)如图![]() ,
, ![]() 为
为![]() 中点,设
中点,设![]() 为线段
为线段![]() 上一点(不含端点),连接
上一点(不含端点),连接![]() .一动点
.一动点![]() 从
从![]() 出发,沿线段
出发,沿线段![]() 以每秒
以每秒![]() 个单位的速度运动到
个单位的速度运动到![]() ,再沿着线段
,再沿着线段![]() 以每秒
以每秒![]() 个单位的速度运动到
个单位的速度运动到![]() 后停止.若点
后停止.若点![]() 在整个运动过程中用时最少,请直接写出最少时间和此时点
在整个运动过程中用时最少,请直接写出最少时间和此时点![]() 的坐标.
的坐标.
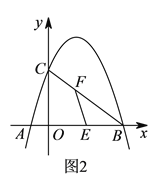
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙![]() 与菱形
与菱形![]() 在平面直角坐标系中,点
在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴上,且点
轴上,且点![]() 在点
在点![]() 的右侧.
的右侧.


(![]() )求菱形
)求菱形![]() 的周长.
的周长.
(![]() )若⊙
)若⊙![]() 沿
沿![]() 轴向右以每秒
轴向右以每秒![]() 个单位长度的速度平移,菱形
个单位长度的速度平移,菱形![]() 沿
沿![]() 轴向左以每秒
轴向左以每秒![]() 个单位长度的速度平移,设菱形移动的时间为(
个单位长度的速度平移,设菱形移动的时间为(![]() 秒),当⊙
秒),当⊙![]() 与
与![]() 相切,且切点为
相切,且切点为![]() 的中点时,连接
的中点时,连接![]() ,求
,求![]() 的值及
的值及![]() 的度数.
的度数.
(![]() )在(
)在(![]() )的条件下,当点
)的条件下,当点![]() 与
与![]() 所在的直线的距离为
所在的直线的距离为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区为了鼓励市民节约用水,计划实行生活用水按阶梯式水价计费,每月用水量不超过10吨(含10吨)时,每吨按基础价收费;每月用水量超过10吨时,超过的部分每吨按调节价收费.例如,第一个月用水16吨,需交水费17.8元,第二个月用水20吨,需交水费23元.
(1)求每吨水的基础价和调节价;
(2)设每月用水量为x吨,应交水费为y元,写出y与x之间的函数关系式;
(3)若某月用水12吨,应交水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点P的坐标为(0,2),直线y= ![]() 与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为( )
与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为( )
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
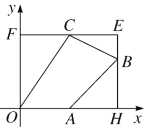
【题目】如图,四边形OABC各个顶点的坐标分别是O(0,0)、A(2,0)、B(4,2)、C(2,3),过点C与![]() 轴平行的直线EF与过点B与
轴平行的直线EF与过点B与![]() 轴平行的直线EH交于点E.
轴平行的直线EH交于点E.
求四边形OABC的面积;
在线段EH上是否存在点P,使四边形OAPC的面积为7?若不存在,说明理由,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com