
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 上的一个动点.
上的一个动点.
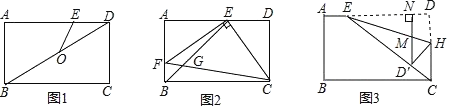
(1)如图1,连接![]() ,
,![]() 是对角线
是对角线![]() 的中点,连接
的中点,连接![]() .当
.当![]() 时,求
时,求![]() 的长;
的长;
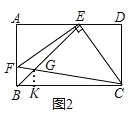
(2)如图2,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,与
,与![]() 交于点
交于点![]() .当
.当![]() 平分
平分![]() 时,求
时,求![]() 的长;
的长;
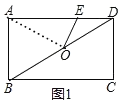
(3)如图3,连接![]() ,点
,点![]() 在
在![]() 上,将矩形
上,将矩形![]() 沿直线
沿直线![]() 折叠,折叠后点
折叠,折叠后点![]() 落在
落在![]() 上的点
上的点![]() 处,过点
处,过点![]() 作
作![]() 于点
于点![]() ,与
,与![]() 交于点
交于点![]() ,且
,且![]() .
.
①求![]() 的值;
的值;
②连接![]() ,
,![]() 与
与![]() 是否相似?请说明理由.
是否相似?请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)①
;(3)①![]() ;②相似,理由见解析.
;②相似,理由见解析.
【解析】
(1)先求出BD,进而求出OD=OB=OA,再判断出△ODE∽△ADO,即可得出结论;
(2)先判断出△AEF≌△DCE,进而求出BF=1,再判断出△CHG∽△CBF,进而求出![]() ,最后用勾股定理即可得出结论;
,最后用勾股定理即可得出结论;
(3)①先求出EC=5,再求出D'C=1,根据勾股定理求出DH=![]() ,CH=
,CH=![]() ,再判断出△EMN∽△EHD,得出
,再判断出△EMN∽△EHD,得出![]() ,△ED'M∽△ECH,得出
,△ED'M∽△ECH,得出![]() ,进而得出
,进而得出![]() ,即可得出结论;
,即可得出结论;
②先判断出∠MD'H=∠NED',进而判断出∠MD'H=∠ECB,即可得出![]() ,即可.
,即可.
(1)如图1,连接![]() ,在矩形
,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]()
在![]() 中,根据勾股定理得,
中,根据勾股定理得,![]() ,
,
∵![]() 是
是![]() 中点,
中点,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴设![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即:![]() ;
;
(2)如图2,在矩形![]() 中,
中,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
∴![]() ,
,
过点![]() 作
作![]() 于
于![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() ,
,
设![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ;
;
(3)①在矩形![]() 中,
中,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
由折叠知,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
设![]() ,
,
∴![]() ,
,
根据勾股定理得,![]() ,
,
∴![]()
![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
②相似,理由:由折叠知,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ∽
∽![]() .
.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】为迎接十二运,某校开设了A:篮球,B:毽球,C:跳绳,D:健美操四种体育活动,为了解学生对这四种体育活动的喜欢情况,在全校范围内随机抽取若干名学生,进行问卷调查(每个被调查的同学必须选择而且只能在4中体育活动中选择一种).将数据进行整理并绘制成以下两幅统计图(未画完整).

(1)这次调查中,一共查了 名学生:
(2)请补全两幅统计图:
(3)若有3名最喜欢毽球运动的学生,1名最喜欢跳绳运动的学生组队外出参加一次联谊互活动,欲从中选出2人担任组长(不分正副),求两人均是最喜欢毽球运动的学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中,有![]() 个红球,
个红球,![]() 个白球,这些球除颜色外都相同.
个白球,这些球除颜色外都相同.
(1)搅匀后从中任意摸出![]() 个球,摸到红球的概率是________;
个球,摸到红球的概率是________;
(2)搅匀后先从中任意摸出![]() 个球(不放回),再从余下的球中任意摸出
个球(不放回),再从余下的球中任意摸出![]() 个球.求两次都摸到红球的概率.(用树状图或表格列出所有等可能出现的结果)
个球.求两次都摸到红球的概率.(用树状图或表格列出所有等可能出现的结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
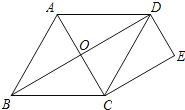
【题目】如图,菱形ABCD的对角线交于点O,点E是菱形外一点,DE∥AC,CE∥BD.
(1)求证:四边形DECO是矩形;
(2)连接AE交BD于点F,当∠ADB=30°,DE=2时,求AF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一款进价为每件40元的护肤品,调查发现,销售单价不低于40元且不高于80元时,该商品的日销售量y(件)与销售单价x(元)之间存在一次函数关系,当销售单价为44元时,日销售量为72件;当销售单价为48元时,日销售量为64件.
(1)求y与x之间的函数关系式;
(2)设该护肤品的日销售利润为w(元),当销售单价x为多少时,日销售利润w最大,最大日销售利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的例题及点拨,并解决问题:
例题:如图①,在等边![]() 中,
中,![]() 是
是![]() 边上一点(不含端点
边上一点(不含端点![]() ),
),![]() 是
是![]() 的外角
的外角![]() 的平分线上一点,且
的平分线上一点,且![]() .求证:
.求证:![]() .
.

点拨:如图②,作![]() ,
,![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() ,得等边
,得等边![]() ,连接
,连接![]() .易证:
.易证:![]() ,可得
,可得![]() ;又
;又![]() ,则
,则![]() ,可得
,可得![]() ;由
;由![]() ,进一步可得
,进一步可得![]() 又因为
又因为![]() ,所以
,所以![]() ,即:
,即:![]() .
.

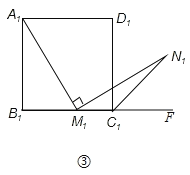
问题:如图③,在正方形![]() 中,
中,![]() 是
是![]() 边上一点(不含端点
边上一点(不含端点![]() ),
),![]() 是正方形
是正方形![]() 的外角
的外角![]() 的平分线上一点,且
的平分线上一点,且![]() .求证:
.求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司研发生产的560件新产品需要精加工后才能投放市场.现由甲、乙两个工厂来加工生产.已知甲工厂每天加工生产的新产品件数是乙工厂每天加工生产新产品件数的1.5倍,并且加工生产240件新产品甲工厂比乙工厂少用4天.
(1)求甲、乙两个工厂每天分别可加工生产多少件新产品?
(2)若甲工厂每天的加工生产成本为3万元,乙工厂每天的加工生产成本为2.4万元,要使这批新产品的加工生产总成本不超过60万元,至少应安排甲工厂加工生产多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
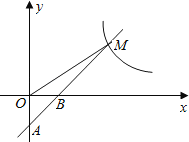
【题目】如图,一次函数y=k1x+b的图象经过A(0,﹣2),B(1,0)两点,与反比例函数![]() 的图象在第一象限内的交点为M,若△OBM的面积为2.
的图象在第一象限内的交点为M,若△OBM的面积为2.
(1)求一次函数和反比例函数的表达式;
(2)在x轴上是否存在点P,使AM⊥MP?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
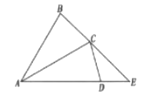
【题目】如图,在△ABC中,AB=AC=4,将△ABC绕点A顺时针旋转30°,得到△ACD,延长AD交BC的延长线于点E,则DE的长为__________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com