
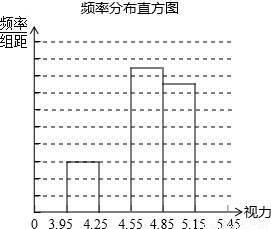
| 频率分布表 | ||
| 分组 | 频数 | 频率 |
| 3.95~4.25 | 6 | 0.12 |
| 4.25~4.55 | a | b |
| 4.55~4.85 | 17 | 0.34 |
| 4.85~5.15 | 15 | 0.3 |
| 5.15~5.45 | 4 | 0.08 |
| 合计 | 50 | 1 |
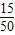 .
.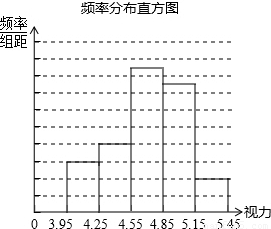 解:(1)a=50-(6+17+15+4)=8,
解:(1)a=50-(6+17+15+4)=8, =300(人).
=300(人).

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2009年上海市南汇区中考数学一模试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2006年全国中考数学试题汇编《二次函数》(09)(解析版) 题型:解答题
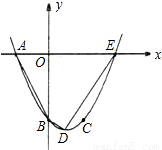
查看答案和解析>>
科目:初中数学 来源:2006年辽宁省十一市中考数学试卷(课标卷)(解析版) 题型:解答题
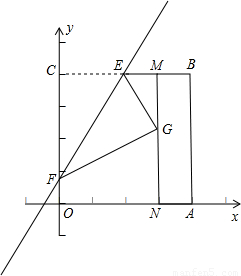
查看答案和解析>>
科目:初中数学 来源:2006年辽宁省十一市中考数学试卷(大纲卷)(解析版) 题型:解答题
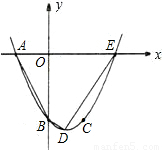
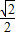 ),以点A为圆心,以AO长为半径的圆交x轴于另一点B,过点B作BF∥AE交⊙A于点F,直线FE交x轴于点C.
),以点A为圆心,以AO长为半径的圆交x轴于另一点B,过点B作BF∥AE交⊙A于点F,直线FE交x轴于点C.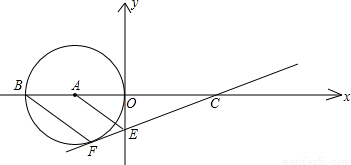
查看答案和解析>>
科目:初中数学 来源:2006年辽宁省十一市中考数学试卷(大纲卷)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com