
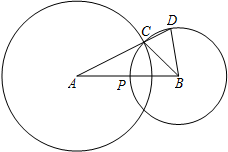
 已知:如图,C是⊙A与⊙B的一个交点,联结AC,并延长交⊙B于点D,⊙B交AB于点P,联结BC、BD,AB=8,AC=6,⊙B的半径为x,线段AD的长为y.
已知:如图,C是⊙A与⊙B的一个交点,联结AC,并延长交⊙B于点D,⊙B交AB于点P,联结BC、BD,AB=8,AC=6,⊙B的半径为x,线段AD的长为y.分析 (1)作BE⊥CD于点E,利用30°的直角△AEB,可得AE的值,就可求出CE的值,由CE=DE,可得CD=2CE即可求出CD的值.
(2)同样利用图1,作BE⊥CD于点E,先得出CE=DE,即可得出CE=$\frac{1}{2}$(AD-AC)=$\frac{1}{2}$(y-6),由⊙B的半径为x,可得OC=x,由BE2=OC2-CE2=AB2-AE2,可得出y关于x的函数解析式,由y>6,写出它的定义域即可;
(3)连接DP,由∠CBD=∠A,∠BDC=∠ADB,可得△BCD∽△ABD,利用相似三角形的面积比等于相似比的平方可得S△BCD:S△ABD=BD2:AD2,由△BDP与△ABD同底为BD,可得S△BDP:S△ABD=BP:AB,即可求出S△BCD:S△BDP的值.
解答 解:(1)如图1,作BE⊥CD于点E,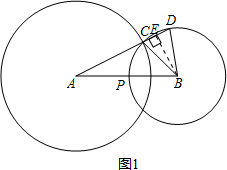
∵∠A=30°,AB=8,
∴AE=4$\sqrt{3}$,
∵AC=6,
∴CE=AE-AC=4$\sqrt{3}$-6,
又∵BC=BD,
∴CE=DE,
∴CD=2CE=2×(4$\sqrt{3}$-6)=8$\sqrt{3}$-12,
(2)如图1,作BE⊥CD于点E,
∵BC=BD,
∴CE=DE,
∴CE=$\frac{1}{2}$(AD-AC)=$\frac{1}{2}$(y-6),
∵⊙B的半径为x,
∴OC=x,
∴BE2=OC2-CE2=x2-$\frac{1}{4}$(y-6)2,
∵BE2=AB2-AE2=64-($\frac{1}{2}$y+3)2,
∴x2-$\frac{1}{4}$(y-6)2=64-($\frac{1}{2}$y+3)2,化简得:y=$-\frac{1}{6}$x2+$\frac{32}{3}$.
(由y>6,得出0<x<2$\sqrt{7}$).
(3)如图2,连接DP,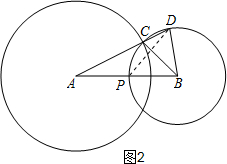
∵∠CBD=∠A,∠BDC=∠ADB,
∴△BCD∽△ABD,
∴S△BCD:S△ABD=BD2:AD2=$\frac{{x}^{2}}{{y}^{2}}$,
∵△BDP与△ABD同底为BD,
∴S△BDP:S△ABD=BP:AB=$\frac{x}{8}$,
∴S△BCD:S△BDP=$\frac{{x}^{2}}{{y}^{2}}$:$\frac{x}{8}$=$\frac{8x}{{y}^{2}}$.
点评 本题主要考查了圆的综合题,涉及含30度角的直角三角形,勾股定理,相似比及二次函数知识等.解题的关键是正确作出辅助线,根据题意列式.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:填空题
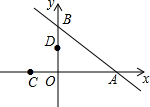 如图,在平面直角坐标系xOy中,直线y=-$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B,将△AOB沿过点A的直线折叠,使点B落在x轴负半轴上,记得点C,折痕与y轴交于点D,则点D的坐标为(0,$\frac{4}{3}$).
如图,在平面直角坐标系xOy中,直线y=-$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B,将△AOB沿过点A的直线折叠,使点B落在x轴负半轴上,记得点C,折痕与y轴交于点D,则点D的坐标为(0,$\frac{4}{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
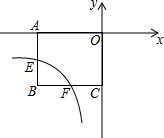 如图,反比例函数y=$\frac{k}{x}$与矩形OABC交于E、F两点,其中E为AB的中点,S△OBF=$\frac{9}{2}$,则k=-6.
如图,反比例函数y=$\frac{k}{x}$与矩形OABC交于E、F两点,其中E为AB的中点,S△OBF=$\frac{9}{2}$,则k=-6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
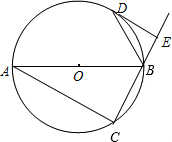 已知:如图,△ABC是⊙O的内角三角形,△ABC的外角平分线BD交⊙O于D,DE与⊙O相切,交CB的延长线于E.
已知:如图,△ABC是⊙O的内角三角形,△ABC的外角平分线BD交⊙O于D,DE与⊙O相切,交CB的延长线于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
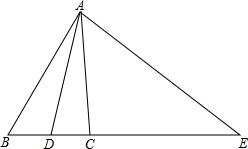 如图所示,在△ABC中,∠EAD=∠EDA,∠EAC=∠B.
如图所示,在△ABC中,∠EAD=∠EDA,∠EAC=∠B.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
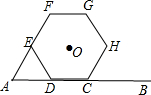 如图,已知线段AB=10,点D从A点开始沿AB边向右运动,以AD为边向上作正△ADE,再以DE为边向右作正六边形DEFGHC,点C恰好落在线段AB上,当C与B重合时运动结束,则正六边形的中心O的运动路径长为5$\sqrt{3}$,点B与点O的最短距离为5.
如图,已知线段AB=10,点D从A点开始沿AB边向右运动,以AD为边向上作正△ADE,再以DE为边向右作正六边形DEFGHC,点C恰好落在线段AB上,当C与B重合时运动结束,则正六边形的中心O的运动路径长为5$\sqrt{3}$,点B与点O的最短距离为5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com