
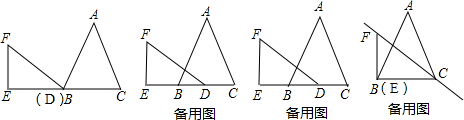
已知等边△ABC和Rt△DEF按如图所示的位置放置,点B,D重合,且点E、B(D)、C在同一条直线上.其中∠E=90°,∠EDF=30°,AB=DE= ,现将△DEF沿直线BC以每秒
,现将△DEF沿直线BC以每秒 个单位向右平移,直至E点与C点重合时停止运动,设运动时间为t秒.
个单位向右平移,直至E点与C点重合时停止运动,设运动时间为t秒.
(1)试求出在平移过程中,点F落在△ABC的边上时的t值;
(2)试求出在平移过程中△ABC和Rt△DEF重叠部分的面积s与t的函数关系式;
(3)当D与C重合时,点H为直线DF上一动点,现将△DBH绕点D顺时针旋转60°得到△ACK,则是否存在点H使得△BHK的面积为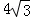 ?若存在,试求出CH的值;若不存在,请说明理由.
?若存在,试求出CH的值;若不存在,请说明理由.
(1)8或10 (2)s=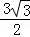 (12﹣t)2 (3)见解析
(12﹣t)2 (3)见解析
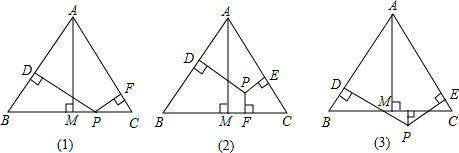
解析试题分析:(1)当F在边AB上时,如图(1),作AM⊥BC,则AM=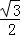 AB=
AB=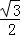 ×6
×6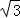 =9,
=9,
∵AM⊥BC,∠FEB=90°
∴EF∥AM,
∴△BEF∽△BMA,
∴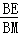 =
=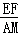 ,即
,即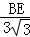 =
= ,解得:BE=2
,解得:BE=2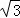 ,则移动的距离是:6
,则移动的距离是:6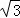 +2
+2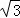 =8
=8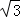 ,则t=
,则t=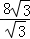 =8;
=8;
当F在AC上时,如图(2)同理可得:EC=2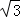 ,则移动的距离是:2×6
,则移动的距离是:2×6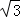 ﹣2
﹣2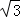 =12
=12 ﹣2
﹣2 =10
=10 ,则t=
,则t=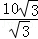 =10,
=10,
故t的值是:8或10;
(2)当0<t≤6时,重合部分是三角形,如图(3),设AB与BE交于点N,
则BD=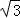 t,
t,
则NB=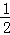 BD=
BD=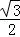 t,ND=
t,ND=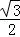 BD=
BD=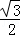 ×
× t=
t=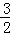 t,则s=
t,则s= NB•ND=
NB•ND= ×
×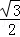 t×
t×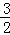 t=
t=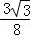 t2;
t2;
当6<t<10时,如图(4),则CD= t﹣6
t﹣6 ,
,
∵∠TCB=60°,∠D=30°
∴∠DTC=30°,
∴∠D=∠DTC,
∴TC=CD= t﹣6
t﹣6 ,
,
则在直角△THC中,TH=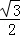 TC=
TC= (
( t﹣6
t﹣6 )=
)=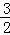 t﹣9,
t﹣9,
则s=18﹣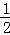 CD•TH=18﹣
CD•TH=18﹣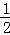 (
( t﹣6
t﹣6 )(
)( t﹣9)=﹣
t﹣9)=﹣ (t﹣6)2+18;
(t﹣6)2+18;
当10≤t<12时,重合部分如图(5),
EC=12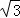 ﹣
﹣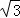 t,
t,
则直角△ECJ中,EJ=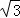 EC=
EC=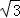 (12
(12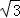 ﹣
﹣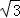 t),
t),
则s=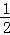 EC•EJ=
EC•EJ=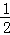 ×
×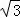 (12
(12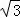 ﹣
﹣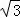 t)2=
t)2=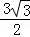 (12﹣t)2.
(12﹣t)2.
(3)当B,H,K在一条直线上时,CH=CK=BC•tan30°=6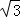 ×
×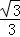 =6,
=6,
设CH=x,作HL⊥BC于点L,则HL= x,
x,
△CKH是边长是x的等边三角形,则面积是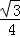 x2,
x2,
△BCH的面积是: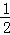 BC•HL=3
BC•HL=3 ×
×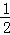 x=
x= x,
x,
△BCK的面积是:3 x.
x.
当0<CH<6时,△BHK的面积=△BCK的面积﹣△CKH的面积﹣△BCH的面积,即3 x﹣
x﹣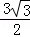 x﹣
x﹣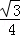 x2=4
x2=4 ,方程无解.
,方程无解.
当CH>6时,△BHK的面积=△CKH的面积+△BCH的面积﹣△BCK的面积,即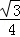 x2+
x2+


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com