
【题目】(解决问题)如图1,在![]() 中,
中,![]() ,
,![]() 于点
于点![]() .点
.点![]() 是
是![]() 边上任意一点,过点
边上任意一点,过点![]() 作
作![]() ,
,![]() ,垂足分别为点
,垂足分别为点![]() ,点
,点![]() .
.
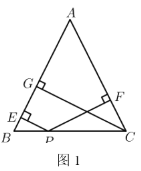
(1)若![]() ,
,![]() ,则
,则![]() 的面积是______,
的面积是______,![]() ______.
______.
(2)猜想线段![]() ,
,![]() ,
,![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
(3)(变式探究)如图2,在![]() 中,若
中,若![]() ,点
,点![]() 是
是![]() 内任意一点,且
内任意一点,且![]() ,
,![]() ,
,![]() ,垂足分别为点
,垂足分别为点![]() ,点
,点![]() ,点
,点![]() ,求
,求![]() 的值.
的值.
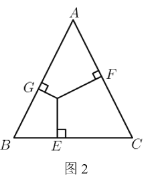
(4)(拓展延伸)如图3,将长方形![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 上,点
上,点![]() 落在点
落在点![]() 处,点
处,点![]() 为折痕
为折痕![]() 上的任意一点,过点
上的任意一点,过点![]() 作
作![]() ,
,![]() ,垂足分别为点
,垂足分别为点![]() ,点
,点![]() .若
.若![]() ,
,![]() ,直接写出
,直接写出![]() 的值.
的值.
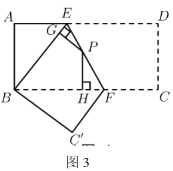
【答案】(1)15,8;(2)![]() ,见解析;(3)
,见解析;(3)![]() ;(4)4
;(4)4
【解析】
解决问题(1)只需运用面积法:![]() ,即可解决问题;
,即可解决问题;
(2)解法同(1);
(3)连接![]() 、
、![]() 、
、![]() ,作
,作![]() 于
于![]() ,由等边三角形的性质得出
,由等边三角形的性质得出![]() ,由勾股定理得出
,由勾股定理得出![]() ,得出
,得出![]() 的面积
的面积![]() ,由
,由![]() 的面积
的面积![]() 的面积
的面积![]() 的面积
的面积![]() 的面积
的面积![]() ,即可得出答案;
,即可得出答案;
(4)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,易证
,易证![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,由解决问题(1)可得
,由解决问题(1)可得![]() ,易证
,易证![]() ,
,![]() ,只需求出
,只需求出![]() 即可.
即可.
解:(1)∵![]() ,
,![]() ,
,![]() ,
,
∴![]() 的面积
的面积![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
且![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
故答案为:15,8.
(2)∵![]() ,
,![]() ,
,![]() ,
,
且![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
(3)连接![]() 、
、![]() 、
、![]() ,作
,作![]() 于
于![]() ,如图2所示:
,如图2所示:
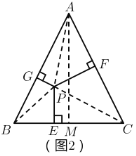
∵![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 的面积
的面积![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() 的面积
的面积![]() 的面积
的面积![]() 的面积
的面积![]() 的面积
的面积
![]()
![]()
![]() ,
,
∴![]() .
.
(4)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,如图3所示:
,如图3所示:
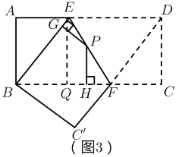
∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
由折叠可得:![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
由解决问题(1)可得:![]() ,
,
∴![]() ,即
,即![]() 的值为4.
的值为4.


科目:初中数学 来源: 题型:
【题目】已知![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,点
,点![]() 是
是![]() 的中点,延长
的中点,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() (如图①).
(如图①).

(1)求证:![]() ≌
≌![]() ;
;
(2)已知点![]() 是
是![]() 的中点,连接
的中点,连接![]() (如图②).
(如图②).
①求证:![]() ≌
≌![]() ;
;
②如图③,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读探索题:
(1)如图1,OP是∠MON的平分线,以O为圆心任意长为半径作弧,分别交射线ON、OM于C、B两点,在射线OP上任取一点A(点O除外),连接AB、AC.求证:△AOB≌△AOC.
(2)请你参考以上方法,解答下列问题:
如图2,在 Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB,试判断BC和AC、AD之间的数量关系并证明.
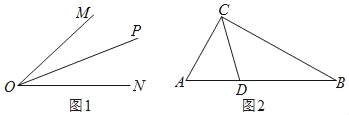
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.
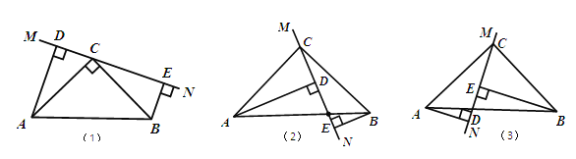
(1)当直线MN绕点C旋转到图(1)的位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到图(2)的位置时,求证:DE=AD-BE;
(3)当直线MN绕点C旋转到图(3)的位置时,试问:DE,AD,BE有怎样的等量关系?请写出这个等量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程(组)解应用题:
为顺利通过国家义务教育均衡发展验收,我市某中学配备了两个多媒体教室,购买了笔记本电脑和台式电脑共120台,购买笔记本电脑用了7.2万元,购买台式电脑用了24万元,已知笔记本电脑单价是台式电脑单价的1.5倍,那么笔记本电脑和台式电脑的单价各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,作ED⊥EB交AB于点D,⊙O是△BED的外接圆.
(1)求证:AC是⊙O的切线;
(2)已知⊙O的半径为2.5,BE=4,求BC,AD的长.
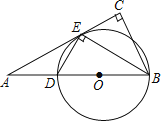
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
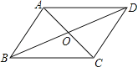
A.AB∥CD,AD∥BCB.OA=OC,OB=OD
C.AD=BC,AB∥CDD.AB=CD,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
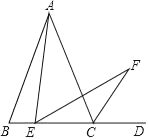
【题目】如图,在△ABC中,AB=AC=2![]() ,BC=4.点E为BC边上一动点,连接AE,作∠AEF=∠B,EF与△ABC的外角∠ACD的平分线交于点F.当EF⊥AC时,EF的长为_______.
,BC=4.点E为BC边上一动点,连接AE,作∠AEF=∠B,EF与△ABC的外角∠ACD的平分线交于点F.当EF⊥AC时,EF的长为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com