练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，抛物线与交于点A（1，3），过点A作x轴的平行线，分别交两条抛物线于点B，C.下列结论：①；②时，；③平行于x轴的直线与两条抛物线有四个交点；④2AB=3AC．其中错误结论的个数是（   ）

    A．1      B．2      C．3           D．4

    B．

    解析试题分析：①把A（1，3）代入，抛物线y1=a（x+2）2﹣3得，3=a（1+2）2﹣3，解得a=，故本选项正确；
    ②由两函数图象可知，抛物线y1=a（x+2）2﹣3
    解析式为y1=（x+2）2﹣3，
    当x=0时，y1=（0+2）2﹣3=﹣，y2=（0﹣3）2+1=，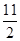
    故y2﹣y1=﹣﹣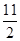=﹣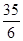，故本选项错误；
    ③当m=3时，平行于x轴的直线与两条抛物线有三个交点，故本选项错误；
    ④∵物线y1=a（x+2）2﹣3与y2=（x﹣3）2+1交于点A（1，3），
    ∴y1的对称轴为x=﹣2，y2的对称轴为x=3，
    ∴B（﹣5，3），C（5，3）
    ∴AB=6，AC=4，
    ∴2AB=3AC，故本选项题正确．
    错误结论的个数是2个．
    故选B．
    考点：二次函数综合题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    “丹棱冻粑”是眉山著名特色小吃，产品畅销省内外，现有一个产品销售点在经销时发现：如果每箱产品盈利10元，每天可售出50箱；若每箱产品涨价1元，日销售量将减少2箱．
    （1）现该销售点每天盈利600元，同时又要顾客得到实惠，那么每箱产品应涨价多少元？
    （2）若该销售点单纯从经济角度考虑，每箱产品应涨价多少元才能获利最高？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    在平面直角坐标系中, 抛物线+与直线交于A, B两点，点A在点B的左侧.
    (1)如图1，当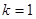时，直接写出A，B两点的坐标；
    (2)在(1)的条件下，点P为抛物线上的一个动点，且在直线AB下方，试求出△ABP面积的最大值及此时点P的坐标；
    (3)如图2，抛物线+ 与轴交于C，D两点（点C在点D的左侧）.在直线上是否存在唯一一点Q，使得∠OQC=90°？若存在，请求出此时的值；若不存在，请说明理由.

    图1                                   图2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    已知：矩形ABCD中，M为BC边上一点， AB=BM=10，MC=14，如图1，正方形EFGH的顶点E和点B重合，点F、G、H分别在边AB、AM、BC上.如图2，P为对角线AC上一动点，正方形EFGH从图1的位置出发，以每秒1个单位的速度沿BC向点C匀速移动；同时，点P从C点出发，以每秒1个单位的速度沿CA向点A匀速移动.当点F到达线段AC上时，正方形EFGH和点P同时停止运动.设运动时间为t秒，解答下列问题：
    （1）在整个运动过程中，当点F落在线段AM上和点G落在线段AC上时，分别求出对应t的值；
    （2）在整个运动过程中，设正方形与重叠部分面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围；
    （3）在整个运动过程中，是否存在点P,使是以DG为腰的等腰三角形？若存在，求出t的值；若不存在，说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上，O为坐标原点，A、B两点的坐标分别为(－3，0)、(0，4)，抛物线y＝x2＋bx＋c经过点B，且顶点在直线x＝上．
    (1)求抛物线对应的函数关系式；
    (2)若把△ABO沿x轴向右平移得到△DCE，点A、B、O的对应点分别是D、C、E，当四边形ABCD是菱形时，试判断点C和点D是否在该抛物线上，并说明理由；
    (3)在(2)的条件下，连接BD，已知对称轴上存在一点P使得△PBD的周长最小，求出P点的坐标；
    (4)在(2)、(3)的条件下，若点M是线段OB上的一个动点(点M与点O、B不重合)，过点M作MN∥BD交x轴于点N，连接PM、PN，设OM的长为t，△PMN的面积为S，求S和t的函数关系式，并写出自变量t的取值范围，S是否存在最大值？若存在，求出最大值和此时M点的坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，直线y＝x＋m与抛物线y＝x2－2x＋l交于不同的两点M、N（点M在点N的左侧）．
    (1)设抛物线的顶点为B，对称轴l与直线y＝x＋m的交点为C，连结BM、BN，若S△MBC＝S△NBC，求直线MN的解析式；
    (2)在(1)条件下，已知点P(t，0)为x轴上的一个动点，
    ①若△PMN为直角三角形，求点P的坐标．
    ②若∠MPN>90°，则t的取值范围是     ．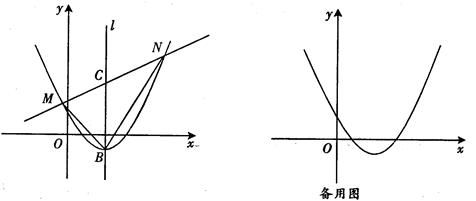

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

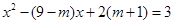    已知关于的方程：①和②，其中.
    （1）求证：方程①总有两个不相等的实数根；
    （2）设二次函数的图象与轴交于、两点（点在点的左侧），将、两点按照相同的方式平移后，点落在点处，点落在点处，若点的横坐标恰好是方程②的一个根，求的值；
    （3）设二次函数，在（2）的条件下，函数，的图象位于直线左侧的部分与直线（）交于两点，当向上平移直线时，交点位置随之变化，若交点间的距离始终不变，则的值是________________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图①，已知二次函数的解析式是y＝ax2＋bx(a>0)，顶点为A(1，－1)．
    (1)a＝   ；
    (2)若点P在对称轴右侧的二次函数图像上运动，连结OP，交对称轴于点B，点B关于顶点A的对称点为C，连接PC、OC，求证：∠PCB＝∠OCB；
    (3)如图②，将抛物线沿直线y＝－x作n次平移(n为正整数，n≤12)，顶点分别为A1，A2，…，An，横坐标依次为1，2，…，n，各抛物线的对称轴与x轴的交点分别为D1，D2，…，Dn，以线段AnDn为边向右作正方形AnDnEnFn，是否存在点Fn恰好落在其中的一个抛物线上，若存在，求出所有满足条件的正方形边长；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    在平面直角坐标系xOy中，直线分别与x轴，y轴交于过点A，B，点C是第一象限内的一点，且AB=AC，AB⊥AC，抛物线经过A，C两点，与轴的另一交点为D．
    （1）求此抛物线的解析式；
    （2）判断直线AB与CD的位置关系，并证明你的结论；
    （3）点M为x轴上一动点，在抛物线上是否存在一点N，使以A,B,M,N四点构成的四边形为平行四边形？若存在，求点N的坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案