证明:(1)如图1,∵a=

,b=1,c=2.
∴c
2=a
2+b
2,c=2b
∴∠C=90°,
∴∠B=30°,
∴∠A=2∠B=60°.
∴△ABC为倍角三角形;
(2)∵∠A=2∠B
∴∠C=180°-∠A-∠B=180°-3∠B
由正弦定理得

=

=

=2R,
即a=2RsinA,b=2RsinB,c=2RsinC
∴b(b+c)=2RsinB(2RsinB+2RsinC),
=4R
2sinB[sinB+sin(180°-3∠B)]
=4R
2sinB(sinB+sin3∠B)
=4R
2sinB(2sin2BcosB)
=4R
2sin2B×sin2B
=4R
2sin
22B
又∵a
2=4R
2sin
2A=4R
2sin
22B
∴a
2=b(b+c);
(3)∵在△ABC中,若∠C=2∠A,
∴由(2)中的结论知c
2=a(a+b);
∵2∠A=4∠B,即∠A=2∠B,
∴a
2=b(b+c),
∴
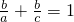
.
分析:(1)利用勾股定理的逆定理求得△ABC为直角三角形,然后根据“30度角所对的直角边是斜边的一半”求得三角形的三个内角,所以根据“倍角三角形”的定义进行证明即可;
(2)根据已知表示各角的度数,再根据正弦定理对式子进行整理,从而得到结论;
(3)利用(2)中的结论进行证明.
点评:本题考查了勾股定理、解直角三角形及正弦定理的内容,综合考察的知识点较多,难度较大,解答本题需要同学们能活学活用.

 ,b=1,c=2.求证:△ABC为倍角三角形﹔
,b=1,c=2.求证:△ABC为倍角三角形﹔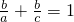 .
.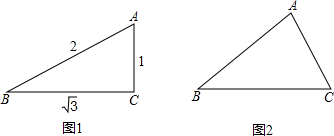
 ,b=1,c=2.
,b=1,c=2. =
= =
= =2R,
=2R,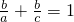 .
.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案