练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在平面直角坐标系 中，双曲线 与直线 交于点A（3，1）．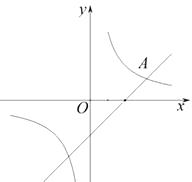

    （1）求直线和双曲线的解析式；
    （2）直线 与x轴交于点B，点P是双曲线 上一点，过点P作直线PC∥x轴，交y轴于点C，交直线 于点D．若DC=2OB，直接写出点 的坐标为 ．

    【答案】
    （1）解：∵直线 过点A（3， 1），

    ∴ ．

    ∴ ．

    ∴直线的解析式为 ．

    ∵双曲线 过点A（3，1），

    ∴ ．

    ∴双曲线的解析式为


    （2） 或
    【解析】解：（2）①∵PC//x轴，DC=2OB，

    ∴ ，

    ∴CF=2OF，

    由直线y=x-2可知F（0.-2），

    ∴OF=2，

    ∴CF=4.

    ∴C的坐标为（0，2）或（0，-6），

    ∴P的纵坐标为2或-6，

    代入y= 得，2= ，解得x= ，-6= ，解得x=- ，

    ∴P（ ，2）或（- ，-6）。

    所以答案是：P（ ，2）或（- ，-6）。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图1,点O在直线MN上,∠AOB=90°,OC平分∠MOB.

    (1)若∠AOC=则∠BOC=_______，∠AOM=_______，∠BON=_________；

    (2)若∠AOC=则∠BON=_______(用含有的式子表示)；

    (3)将∠AOB绕着点O顺时针转到图2的位置,其他条件不变，若∠AOC=(为钝角),求∠BON的度数(用含的式子表示).

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知四边形ABCD为等腰梯形，AD∥BC，AB=CD，AD= ，E为CD中点，连接AE，且AE=2 ，∠DAE=30°，作AE⊥AF交BC于F，则BF=（ ）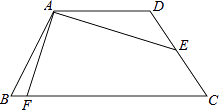

    A.1
    B.3﹣
    C. ﹣1
    D.4﹣2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

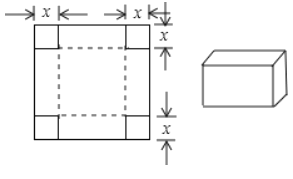
    【题目】如图所示，一张边长为的正方形硬纸板，把它的四个角都剪去一个边长为工(为正整数)的小正方形，然后把它折成一个无盖的长方体，设长方体的容积为，请回答下列问题：

    （1）用含有的代数式表示，则

    （2）完成下表：

    1

    2

    3

    4

    5

    6

    7

    （3）观察上表，当取什么值时，容积的值最大？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

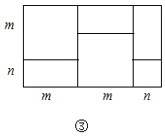
    【题目】如图①是一个长为、宽为的长方形，沿图中虛线用剪刀平均分成四块小长方形，然后按图②的形状拼成一个正方形．

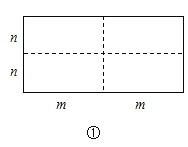
    （1）图②中的阴影部分的面积为

    （2）观察图②，请你写出代数式与之间的等量关系式

    （3）若则

    （4）实际上有许多代数恒等式可以用图形的面积来表示．如图③，它表示

    （5）试画出一个几何图形，使它的面积能表示

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系 中，定义直线 与双曲线 的交点 （m、n为正整数）为 “双曲格点”，双曲线 在第一象限内的部分沿着竖直方向平移或以平行于 轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”．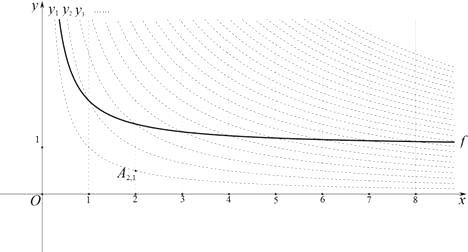

    （1）①“双曲格点” 的坐标为；
    ②若线段 的长为1个单位长度，则n=；
    （2）图中的曲线 是双曲线 的一条“派生曲线”，且经过点 ，则 的解析式为 y=；
    （3）画出双曲线 的“派生曲线”g（g与双曲线 不重合），使其经过“双曲格点” 、 、 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在平面直角坐标系xoy中，一次函数y= x+3的图象与x轴和y轴交于A、B两点，将△AOB绕点O顺时针旋转90°后得到△A′OB′．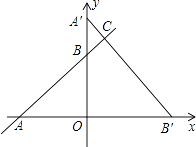

    （1）求直线A′B′的解析式；
    （2）若直线A′B′与直线AB相交于点C，求S△ABC：S△ABO的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，数轴上，O点与C点对应的数分别是0、60（单位：单位长度），将一根质地均匀的直尺AB放在数轴上（A在B的左边），若将直尺在数轴上水平移动，当A点移动到B点的位置时，B点与C点重合，当B点移动到A点的位置时，A点与O点重合．

    （1）直尺的长为多少个单位长度（直接写答案）

    （2）如图2，直尺AB在数轴上移动，有BC=4OA，求此时A点对应的数；

    （3）如图3，以OC为边搭一个横截面为长方形的不透明的篷子，将直尺放入篷内的数轴上的某处（看不到直尺的任何部分，A在B的左边），将直尺AB沿数轴以5个单位/秒的速度分别向左、向右移动，直到完全看到直尺，所经历的时间为t1、t2， 若t1﹣t2=2（秒），求直尺放入蓬内，A点对应的数为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】

    （1）如图1，在正方形ABCD中，M是BC边（不含端点B、C）上任意一点，P是BC延长线上一点，N是∠DCP的平分线上一点．若∠AMN=90°，求证：AM=MN．

    下面给出一种证明的思路，你可以按这一思路证明，也可以选择另外的方法证明．

    证明：在边AB上截取AE=MC，连ME．正方形ABCD中，∠B=∠BCD=90°，AB=BC．

    ∴∠NMC=180°—∠AMN—∠AMB=180°—∠B—∠AMB=∠MAB=∠MAE．

    （下面请你完成余下的证明过程）

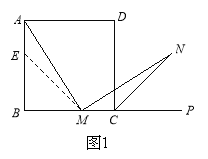
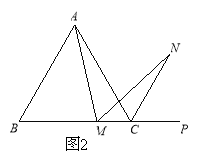
    （2）若将（1）中的“正方形ABCD”改为“正三角形ABC”（如图2），N是∠ACP的平分线上一点，则当∠AMN=60°时，结论AM=MN是否还成立？请说明理由．

    （3）若将（1）中的“正方形ABCD”改为“正边形ABCD……X”，请你作出猜想：当∠AMN= °时，结论AM=MN仍然成立．（直接写出答案，不需要证明）

    查看答案和解析>>

    同步练习册答案