
 边上)的一个动点,点C在y轴上,抛物线y=ax2+bx+1以P为顶点.
边上)的一个动点,点C在y轴上,抛物线y=ax2+bx+1以P为顶点. ,这时能确定a、b的值吗?若能,请求出a、b的值;若不能,请确定a、b的取值范围.(本题的图形仅供分析参考用)
,这时能确定a、b的值吗?若能,请求出a、b的值;若不能,请确定a、b的取值范围.(本题的图形仅供分析参考用) (2)如图,设抛物线与x轴的交点坐标为F(x1,0)、E(x2,0),
(2)如图,设抛物线与x轴的交点坐标为F(x1,0)、E(x2,0), OE•OA=
OE•OA= x2;
x2; OF•OA=
OF•OA= x1
x1 x2-(
x2-( x1)=3,即x1+x2=6
x1)=3,即x1+x2=6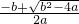 +
+ =
=
 =6,即b=-6a①
=6,即b=-6a①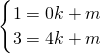 ,解得
,解得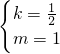 ,∴
,∴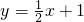
 ,所以纵坐标=
,所以纵坐标=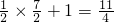
 ,
, )的坐标代入y=ax2+bx+1,
)的坐标代入y=ax2+bx+1, ,
,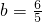 .
. ,求D点纵坐标,代入抛物线解析式,得到a、b的另外一个关系式,解方程组求a、b的值.
,求D点纵坐标,代入抛物线解析式,得到a、b的另外一个关系式,解方程组求a、b的值.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
| 3 |
 =2,∠ADC=30°
=2,∠ADC=30°查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com