
【题目】如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(-4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).

(1)写出∠PBD的度数和点D的坐标(点D的坐标用t表示);
(2)探索△POE周长是否随时间t的变化而变化,若变化,说明理由;若不变,试求这个定值.
(3)当t为何值时,△PBE为等腰三角形?
【答案】(1)45°,(t,t).(2)△POE周长是定值,该定值为8.(3)当t为4秒或(4![]() -4)秒时,△PBE为等腰三角形.
-4)秒时,△PBE为等腰三角形.
【解析】
试题(1)易证△BAP≌△PQD,从而得到DQ=AP=t,从而可以求出∠PBD的度数和点D的坐标;
(2)由于∠EBP=45°,故图1是以正方形为背景的一个基本图形,容易得到EP=AP+CE.容易得到△POE周长等于AO+CO=8,从而解决问题;
(3)EP=AP+CE,由于△PBE底边不定,故分三种情况讨论,借助于三角形全等及勾股定理进行求解,然后结合条件进行取舍,最终确定符合要求的t值.
试题解析:(1)如图1,

由题可得:AP=OQ=1×t=t(秒)
∴AO=PQ.
∵四边形OABC是正方形,
∴AO=AB=BC=OC,
∠BAO=∠AOC=∠OCB=∠ABC=90°.
∵DP⊥BP,
∴∠BPD=90°.
∴∠BPA=90°-∠DPQ=∠PDQ.
∵AO=PQ,AO=AB,
∴AB=PQ.
在△BAP和△PQD中,

∴△BAP≌△PQD(AAS).
∴AP=QD,BP=PD.
∵∠BPD=90°,BP=PD,
∴∠PBD=∠PDB=45°.
∵AP=t,
∴DQ=t.
∴点D坐标为(t,t).
(2)∵∠EBP=45°
∴由图1可以得到EP=CE+AP,
∴OP+PE+OE=OP+AP+CE+OE
=AO+CO
=4+4
=8.
∴△POE周长是定值,该定值为8.
(3)①若PB=PE,
由△PAB≌△DQP得PB=PD,
显然PB≠PE,
∴这种情况应舍去.
②若EB=EP,
则∠PBE=∠BPE=45°.
∴∠BEP=90°.
∴∠PEO=90°-∠BEC=∠EBC.
在△POE和△ECB中,
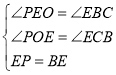
∴△POE≌△ECB(AAS).
∴OE=CB=OC.
∴点E与点C重合(EC=0).
∴点P与点O重合(PO=0).
∵点B(-4,4),
∴AO=CO=4.
此时t=AP=AO=4.
③若BP=BE,
在Rt△BAP和Rt△BCE中,
![]()
∴Rt△BAP≌Rt△BCE(HL).
∴AP=CE.
∵AP=t,
∴CE=t.
∴PO=EO=4-t.
∵∠POE=90°,
∴PE=![]() .
.
延长OA到点F,使得AF=CE,连接BF,如图2所示.
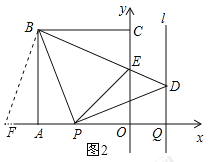
在△FAB和△ECB中,
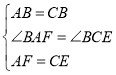
∴△FAB≌△ECB.
∴FB=EB,∠FBA=∠EBC.
∵∠EBP=45°,∠ABC=90°,
∴∠ABP+∠EBC=45°.
∴∠FBP=∠FBA+∠ABP
=∠EBC+∠ABP=45°.
∴∠FBP=∠EBP.
在△FBP和△EBP中,
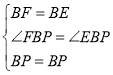
∴△FBP≌△EBP(SAS).
∴FP=EP.
∴EP=FP=FA+AP
=CE+AP.
∴EP=t+t=2t.
∴![]() (4-t)=2t.
(4-t)=2t.
解得:t=4![]() -4
-4
∴当t为4秒或(4![]() -4)秒时,△PBE为等腰三角形.
-4)秒时,△PBE为等腰三角形.


 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
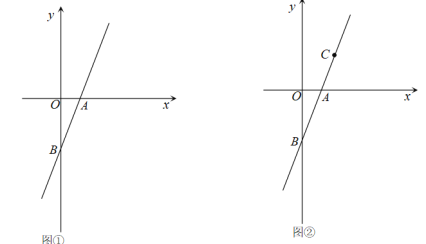
【题目】已知,直线y=2x-2与x轴交于点A,与y轴交于点B.
(1)如图①,点A的坐标为_______,点B的坐标为_______;
(2)如图②,点C是直线AB上不同于点B的点,且CA=AB.
①求点C的坐标;
②过动点P(m,0)且垂直与x轴的直线与直线AB交于点E,若点E不在线段BC上,则m的取值范围是_______;
(3)若∠ABN=45,求直线BN的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程交由甲、乙两个工程队来完成,已知甲工程队单独完成需要60天,乙工程队单独完成需要40天
(1)若甲工程队先做30天后,剩余由乙工程队来完成,还需要用时 天
(2)若甲工程队先做20天,乙工程队再参加,两个工程队一起来完成剩余的工程,求共需多少天完成该工程任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的有( )
①有理数包括正有理数和负有理数; ②绝对值等于它本身的数是非负数;③若|b|=|﹣5|,则b=-5 ; ④当b=2时,5﹣|2b﹣4|有最小值是5;⑤若![]() 、
、![]() 互为相反数,则
互为相反数,则![]() ;⑥
;⑥![]() 是关于
是关于![]() 、
、![]() 的六次三项式.
的六次三项式.
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,CE![]() AD于点E,且CB=CE,点F为CD边上的一点,CB=CF,连接BF交CE于点G.
AD于点E,且CB=CE,点F为CD边上的一点,CB=CF,连接BF交CE于点G.
(1)若![]() ,CF=
,CF=![]() ,求CG的长;
,求CG的长;
(2)求证:AB=ED+CG

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①若a<1,则(a﹣1)![]() =﹣
=﹣![]() ;②圆是中心对称图形又是轴对称图形;③
;②圆是中心对称图形又是轴对称图形;③![]() 的算术平方根是4;④如果方程ax2+2x+1=0有实数根,则实数a≤1.其中正确的命题个数是( )
的算术平方根是4;④如果方程ax2+2x+1=0有实数根,则实数a≤1.其中正确的命题个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“国际象棋”、“音乐舞蹈”和“书法”等说个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了本校部分学生选择社团的意向.并将调查结果绘制成如下统计图表(不完整):
选择意向 | 文学鉴赏 | 国际象棋 | 音乐舞蹈 | 书法 | 其他 |
所占百分比 | a | 20% | b | 10% | 5% |
根据统计图表的信息,解答下列问题:
(1)求本次抽样调查的学生总人数及a、b的值;
(2)将条形统计图补充完整;
(3)若该校共有1200名学生,试估计全校选择“音乐舞蹈”社团的学生人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3)。双曲线![]() 的图像经过BC的中点D,且与AB交于点E,连接DE。
的图像经过BC的中点D,且与AB交于点E,连接DE。

(1)求k的值及点E的坐标;
(2)若点F是边上一点,且△FBC∽△DEB,求直线FB的解析式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在圆![]() 中,
中,![]() 、
、![]() 是圆
是圆![]() 的半径,点
的半径,点![]() 在劣弧弧
在劣弧弧![]() 上,
上,![]() ,
,![]() ,
,![]() ∥
∥![]() ,联结
,联结![]() .
.
(1)如图1,求证:![]() 平分
平分![]() ;
;
(2)点![]() 在弦
在弦![]() 的延长线上,联结
的延长线上,联结![]() ,如果△
,如果△![]() 是直角三角形,请你在如图2中画出
是直角三角形,请你在如图2中画出
点![]() 的位置并求
的位置并求![]() 的长;
的长;
(3)如图3,点![]() 在弦
在弦![]() 上,与点
上,与点![]() 不重合,联结
不重合,联结![]() 与弦
与弦![]() 交于点
交于点![]() ,设点
,设点![]() 与点
与点![]() 的
的
距离为![]() ,△
,△![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围.
的取值范围.



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com