练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，AB是⊙O的直径，AC是⊙O的弦，过点C的切线交AB的延长线于点D，若∠A=∠D，CD=3，则图中阴影部分的面积为 ．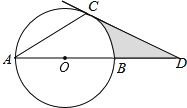

    【答案】
    【解析】解：连接OC，
    ∵过点C的切线交AB的延长线于点D，
    ∴OC⊥CD，
    ∴∠OCD=90°，
    即∠D+∠COD=90°，
    ∵AO=CO，
    ∴∠A=∠ACO，
    ∴∠COD=2∠A，
    ∵∠A=∠D，
    ∴∠COD=2∠D，
    ∴3∠D=90°，
    ∴∠D=30°，
    ∴∠COD=60°
    ∵CD=3，
    ∴OC=3× = ，∴阴影部分的面积= ×3× ﹣ = ，故答案为： ．

    连接OC，可求得△OCD和扇形OCB的面积，进而可求出图中阴影部分的面积．本题主要考查切线的性质及扇形面积的计算，掌握过切点的半径与切线垂直是解题的关键．求出∠D=30°是解题的突破口．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下列各式中：

    ①由3x＝﹣4系数化为1得x＝﹣；

    ②由5＝2﹣x移项得x＝5﹣2；

    ③由 去分母得2（2x﹣1）＝1+3（x﹣3）；

    ④由2（2x﹣1）﹣3（x﹣3）＝1去括号得4x﹣2﹣3x﹣9＝1．

    其中正确的个数有（　　）

    A. 0个 B. 1个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】模型与应用.

    （模型）

    （1）如图①，已知AB∥CD，求证∠1＋∠MEN＋∠2＝360°.

    （应用）

    （2）如图②，已知AB∥CD，则∠1+∠2+∠3+∠4+∠5+∠6的度数为 ．

    如图③，已知AB∥CD，则∠1+∠2+∠3+∠4+∠5+∠6＋…＋∠n的度数为 ．

    （3）如图④，已知AB∥CD，∠AM1M2的角平分线M1 O与∠CMnMn－1的角平分线MnO交于点O，若∠M1OMn＝m°．

    在（2）的基础上，求∠2+∠3+∠4+∠5+∠6＋……＋∠n－1的度数．（用含m、n的代数式表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC，AB=AC，以AB为直径的⊙O分别交AC、BC于点D、E，点F在AC的延长线上，且∠CBF= ∠CAB．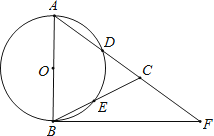
    （1）求证：直线BF是⊙O的切线；
    （2）若AB=5，sin∠CBF= ，求BC和BF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】矩形OABC在平面直角坐标系中的位置如图所示，点B的坐标为（3，4），D是OA的中点，点E在AB上，当△CDE的周长最小时，点E的坐标为（　　）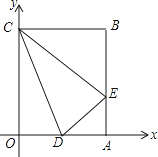

    A.（3，1）
    B.（3， ）
    C.（3， ）
    D.（3，2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）计算

    ①（1﹣）×（1+）=　 　，1﹣（）2=　 　； 有（1﹣）×（1+）　 　1﹣（）2 （用“=”“＜”“＞”填空）．

    ②（1﹣）×（1+）=　 　，1﹣（）2=　 　； 有（1﹣）×（1+）　 　1﹣（）2 （用“=”“＜”“＞”填空）．

    ③猜测（1﹣）（1+）与1﹣（）2 有关系：（1﹣）（1+）　 　1﹣（）2．（用“=”“＜”“＞”填空）

    （2）计算：[1﹣（）2]×[1﹣（）2]×[1﹣（）2]×…×[1﹣（）2]

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一次函数y=kx+b的图象与x轴交于点A，与反比例函数y= （x＞0）的图象交于点B（2，n），过点B作BC⊥x轴于点C，点P（3n﹣4，1）是该反比例函数图象上的一点，且∠PBC=∠ABC，求反比例函数和一次函数的表达式．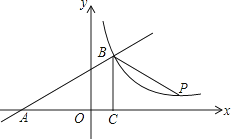

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一元二次方程 +2 x-6=0的根是（　　）
    A. = =
    B. =0， =-2
    C. = ， =-3
    D. =- ， =3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题情境：如图1，AB∥CD，∠PAB＝130°，∠PCD＝120°，求∠APC的度数．

    小明的思路是：如图2，过P作PE∥AB，通过平行线性质，可得∠APC＝50°＋60°＝110°.

    问题迁移：

    (1)如图3，AD∥BC，点P在射线OM上运动，当点P在A、B两点之间运动时，∠ADP＝∠α，∠BCP＝∠β.∠CPD、∠α、∠β之间有何数量关系？请说明理由；

    (2)在(1)的条件下，如果点P在A、M两点之间和B、O两点之间上运动时(点P与点A、B、O三点不重合)，请你分别直接写出∠CPD、∠α、∠β之间的数量关系．

    ,图1)　,图2)

    ,图3)　,备用图)

    查看答案和解析>>

    同步练习册答案