
如图1,在Rt△AOB中,∠AOB=90°,AO= ,∠ABO=30°.动点P在线段AB上从点A向终点B以每秒
,∠ABO=30°.动点P在线段AB上从点A向终点B以每秒 个单位的速度运动,设运动时间为t秒.在直线OB 上取两点M、N作等边△PMN.
个单位的速度运动,设运动时间为t秒.在直线OB 上取两点M、N作等边△PMN.
(1)求当等边△PMN的顶点M运动到与点O重合时t的值.
(2)求等边△PMN的边长(用t的代数式表示);
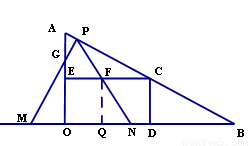
(3)如果取OB的中点D,以OD为边在Rt△AOB 内部作如图2所示的矩形ODCE,点C在线段AB上.设等边△PMN和矩形ODCE重叠部分的面积为S,请求出当0≤t≤2秒时S与t的函数关系式,并求出S的最大值.
(4)在(3)中,设PN与EC的交点为R,是否存在点R,使△ODR是等腰三角形?若存在,求出对应的t的值;若不存在,请说明理由.

解:(1)当等边△PMN的顶点M运动到与点O重合时,
MP⊥AB,∵∠A=60°,∴AP=4 ,∴
,∴ 。(2分)
。(2分)

(2)∵AP= ,∴BP=
,∴BP=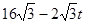
又∵∠B=30°,∠PMB=600°,∴∠BPM=90°
tan∠B=
∴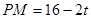 ,即等边△PMN的边长为
,即等边△PMN的边长为 .(4分)
.(4分)
(3)①当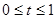 时,如图AP=
时,如图AP= ,∴
,∴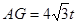
∴ ,∴
,∴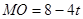 ,
,
∴ .
.
过F作FQ⊥0B于Q,则QN=4,∴EF=OQ= .
.
等边△PMN和矩形ODCE重叠部分的面积为四边形EFNO的面积,设为S1,
∴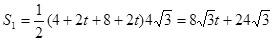
∵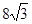 >0,∴S1随t的增大而增大,
>0,∴S1随t的增大而增大,
∴t=1时,,∴S1的最大值为 .(7分)
.(7分)
②当 <t<2时,如图
<t<2时,如图
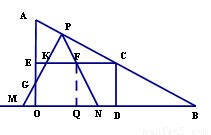
在△EGK中,GE= ,∴EK=
,∴EK= ,
,
∴S△GEK= .
.
∴等边△PMN和矩形ODCE重叠部分的面积为四边形EFNO的面积与△EGK的面积差,设为S2,
∴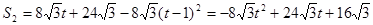 .
.
∵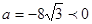 ,对称轴为
,对称轴为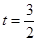 ,
,
∴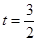 时,
时,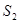 的最大值为
的最大值为 .(9分)
.(9分)
当 时,
时,
 。
。
综上可知:当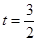 时,S的最大值为
时,S的最大值为 .(10分)
.(10分)
(4)过R作RH⊥OB于H,RH= ,HN=4,
,HN=4,

OH= ,OD=12,DH=
,OD=12,DH= ,
,
①OR=OD=12时,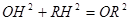 ,
,
∴ ,
, ,∴
,∴ >2,不合题意舍去。
>2,不合题意舍去。
②DR=OD=12时, ,
,
∴ ,∴
,∴ >2,或
>2,或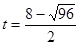 <0,都不合题意舍去。
<0,都不合题意舍去。
③OR=DR时,H为CD中点,OH=6,∴ ,∴
,∴ 。
。
综上所述, 时,△ODR是等腰三角形。(12分)
时,△ODR是等腰三角形。(12分)
【解析】(1)利用直角三角形中30°所对的边是斜边的一半即可求出AP,进而求出t的值;
(2)利用△BPH∽△BAO,得出PH的长,再利用解直角三角形求出PN的长;
(3)根据当0≤t≤1时以及当t=1时和当t=2时,分别求出S的值;
(4)根据当D为顶点,OD=OR1=6时,当R2为顶点,OR2=DR2时,③当O为等腰△的顶点时,分别得出即可


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2012届重庆全善学校九年级下学期第二次月考数学试卷(带解析) 题型:解答题
如图1,在Rt△AOB中,∠AOB=90°,AO= ,∠ABO=30°.动点P在线段AB上从点A向终点B以每秒
,∠ABO=30°.动点P在线段AB上从点A向终点B以每秒 个单位的速度运动,设运动时间为t秒.在直线OB 上取两点M、N作等边△PMN.
个单位的速度运动,设运动时间为t秒.在直线OB 上取两点M、N作等边△PMN.
(1)求当等边△PMN的顶点M运动到与点O重合时t的值.
(2)求等边△PMN的边长(用t的代数式表示);
(3)如果取OB的中点D,以OD为边在Rt△AOB 内部作如图2所示的矩形ODCE,点C在线段AB上.设等边△PMN和矩形ODCE重叠部分的面积为S,请求出当0≤t≤2秒时S与t的函数关系式,并求出S的最大值.
(4)在(3)中,设PN与EC的交点为R,是否存在点R,使△ODR是等腰三角形?若存在,求出对应的t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 ,∠ABO=30°.动点P在线段AB上从点A向终点B以每秒
,∠ABO=30°.动点P在线段AB上从点A向终点B以每秒 个单位的速度运动,设运动时间为t秒.在直线OB 上取两点M、N作等边△PMN.
个单位的速度运动,设运动时间为t秒.在直线OB 上取两点M、N作等边△PMN.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com