
【题目】如图,在平面直角坐标系中,点![]() 是
是![]() 轴正半轴上的一动点,抛物线
轴正半轴上的一动点,抛物线![]() (
(![]() 是常数,且
是常数,且![]() 过点
过点![]() ,与
,与![]() 轴交于
轴交于![]() 两点,点
两点,点![]() 在点
在点![]() 左侧,连接
左侧,连接![]() ,以
,以![]() 为边做等边三角形
为边做等边三角形![]() ,点
,点![]() 与点
与点![]() 在直线
在直线![]() 两侧.
两侧.
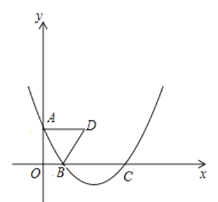
(1)求B、C的坐标;
(2)当![]() 轴时,求抛物线的函数表达式;
轴时,求抛物线的函数表达式;
(3)①求动点![]() 所成的图像的函数表达式;
所成的图像的函数表达式;
②连接![]() ,求
,求![]() 的最小值.
的最小值.
科目:初中数学 来源: 题型:
【题目】抛物线y=x2+bx+c的图象经过点A(﹣1,0),B(0,﹣3).
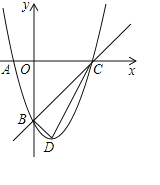
(1)求这个抛物线的解析式;
(2)抛物线与x轴的另一交点为C,抛物线的顶点为D,判断△CBD的形状;
(3)直线BN∥x轴,交抛物线于另一点N,点P是直线BN下方的抛物线上的一个动点(点P不与点B和点N重合),过点P作x轴的垂线,交直线BC于点Q,当四边形BPNQ的面积最大时,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,点
,点![]() 是抛物线的顶点,过点
是抛物线的顶点,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,连接
,连接![]() .
.
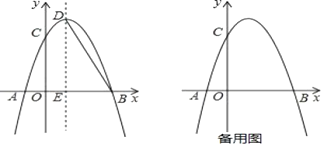
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)点![]() 是抛物线上的动点,当
是抛物线上的动点,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)若点![]() 是
是![]() 轴上方抛物线上的动点,以
轴上方抛物线上的动点,以![]() 为边作正方形
为边作正方形![]() ,随着点
,随着点![]() 的运动,正方形的大小、位置也随着改变,当顶点
的运动,正方形的大小、位置也随着改变,当顶点![]() 或
或![]() 恰好落在
恰好落在![]() 轴上时,请直接写出点
轴上时,请直接写出点![]() 的横坐标.
的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,动点E从A出发,沿A→B→C方向运动,当点E到达点C时停止运动,过点E作EF⊥AE交CD于点F,设点E运动路程为x,CF=y,如图2所表示的是y与x的函数关系的大致图象,给出下列结论:①a=3;②当CF=![]() 时,点E的运动路程为
时,点E的运动路程为![]() 或
或![]() 或
或![]() ,则下列判断正确的是( )
,则下列判断正确的是( )
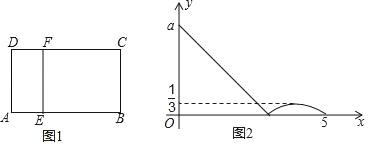
A. ①②都对 B. ①②都错 C. ①对②错 D. ①错②对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郴州市正在创建“全国文明城市”,某校拟举办“创文知识”抢答赛,欲购买A、B两种奖品以鼓励抢答者.如果购买A种20件,B种15件,共需380元;如果购买A种15件,B种10件,共需280元.
(1)A、B两种奖品每件各多少元?
(2)现要购买A、B两种奖品共100件,总费用不超过900元,那么A种奖品最多购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD与AB相交,连接CO,过点D作⊙O的切线,与AB的延长线交于点E,若DE∥AC,∠BAC=40°,则∠OCD的度数为( )
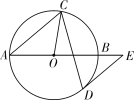
A.65°B.30°C.25°D.20°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,且对角线AC⊥BD,垂足为点E,过点C作CF⊥AB于点F,交BD于点G.
(1)如图①,连接EF,若EF平分∠AFG,求证:AE=GE;
(2)如图②,连接CO并延长交AB于点H,若CH为∠ACF的平分线,AD=3,且tan∠FBG=![]() ,求线段AH长
,求线段AH长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于![]() 的一元二次方程
的一元二次方程![]() 有两个实数根,且其中一根为另一根的2倍,则称这样的方程为“倍根方程”,以下关于倍根方程的说法,不正确的是( )
有两个实数根,且其中一根为另一根的2倍,则称这样的方程为“倍根方程”,以下关于倍根方程的说法,不正确的是( )
A.方程![]() 是倍根方程;
是倍根方程;
B.若![]() 是倍根方程,则
是倍根方程,则![]() ;
;
C.若方程![]() 是倍根方程,且相异两点
是倍根方程,且相异两点![]() 都在抛物线
都在抛物线![]() 上,则方程
上,则方程![]() 的一个根为
的一个根为![]() ;
;
D.若点![]() 在反比例函数
在反比例函数![]() 的图象上,则关于
的图象上,则关于![]() 的方程
的方程![]() 是倍根方程.
是倍根方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
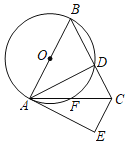
【题目】如图,在△ABC中,AB=BC,以AB为直径的⊙O交BC于点D,交AC于点F,过点C作CE∥AB,且∠CAD=∠CAE.
(1)求证:AE是⊙O的切线;
(2)若AB=8,AC=6,求CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com