
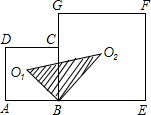
 如图,边长为a的正方形ABCD和边长为b的正方形BEFG排放在一起,O1和O2分别是两个正方形的中心,则阴影部分的面积为
如图,边长为a的正方形ABCD和边长为b的正方形BEFG排放在一起,O1和O2分别是两个正方形的中心,则阴影部分的面积为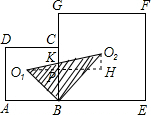 解:做O1H∥AE,使O2H⊥O1H,交BG于P,K点,
解:做O1H∥AE,使O2H⊥O1H,交BG于P,K点,| 1 |
| 2 |
| KP |
| HO2 |
| PO1 |
| HO1 |
| a |
| a+b |
| a |
| a+b |
| b-a |
| 2 |
| ab-a2 |
| 2(a+b) |
| 1 |
| 2 |
| a+b |
| 2 |
| 1 |
| 2 |
| a |
| 2 |
| ab-a2 |
| 2(a+b) |
| a+b |
| 2 |
| 2ab |
| 8 |
| ab |
| 4 |
| a+b |
| 2 |
| b-a |
| 2 |
| HO12+HO22 |
|
| 1 |
| 2 |
| 2(a2+ b2) |
| ab |
| 4 |
| 1 |
| 2 |
| 2(a2+ b2) |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.
如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.
如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.查看答案和解析>>
科目:初中数学 来源:2012-2013学年新人教版九年级(上)期中数学试卷(7)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com