
【题目】阅读理解:给定一个矩形,如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的一半,则这个矩形是给定矩形的“减半”矩形.如图,矩形![]() 是矩形
是矩形![]() 的“减半”矩形.
的“减半”矩形.
请你解决下列问题:
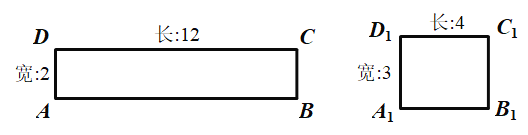
(1)当矩形的长和宽分别为![]() ,
,![]() 时,它是否存在“减半”矩形?请作出判断,并说明理由.
时,它是否存在“减半”矩形?请作出判断,并说明理由.
(2)边长为![]() 的正方形存在“减半”正方形吗?如果存在,求出“减半”正方形的边长;如果不存在,请说明理由.
的正方形存在“减半”正方形吗?如果存在,求出“减半”正方形的边长;如果不存在,请说明理由.
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
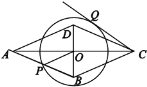
【题目】如图,菱形ABCD中,对角线AC和BD相交于点O,AC=10,BD=4,动点P在边AB上运动,以点O为圆心,OP为半径作⊙O,CQ切⊙O于点Q,则在点P运动过程中,CQ的长的最大值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 在
在![]() 轴正半轴上,
轴正半轴上,![]() 轴,点
轴,点![]() 的横坐标都是
的横坐标都是![]() ,且
,且![]() ,点
,点![]() 在
在![]() 上,若反比例函数
上,若反比例函数![]() 的图象经过点
的图象经过点![]() ,且
,且![]() .
.
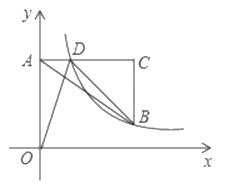
(1)求点![]() 坐标;
坐标;
(2)将![]() 沿着
沿着![]() 折叠,设顶点
折叠,设顶点![]() 的对称点为
的对称点为![]() ,试判断点
,试判断点![]() 是否恰好落在直线
是否恰好落在直线![]() 上,为什么.
上,为什么.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】取三张形状大小一样,质地完全的相同卡片,在三张卡片上分别写上“李明、王强、孙伟”这三个同学的名字,然后将三张卡片放入一个不透明的盒子里.
(1)林老师从盒子中任取一张,求取到写有李明名字的卡片概率是多少?
(2)林老师从盒子中取出一张卡片,记下名字后放回,再从盒子中取出第二张卡片,记下名字.用列表或画树形图列出林老师取到的卡片的所有可能情况,并求出两次都取到写有李明名字的卡片的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
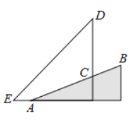
【题目】在屋楼崮西侧一个坡度(或坡比)![]() 的山坡
的山坡![]() 上发现有一棵古树
上发现有一棵古树![]() .测得古树底端
.测得古树底端![]() 到山脚点
到山脚点![]() 的距离
的距离![]() 米,在距山脚点
米,在距山脚点![]() 水平距离
水平距离![]() 米的点
米的点![]() 处,测得古树顶端
处,测得古树顶端![]() 的仰角
的仰角![]() (古树
(古树![]() 与山坡
与山坡![]() 的剖面、点
的剖面、点![]() 在同一平面上,古树
在同一平面上,古树![]() 与直线
与直线![]() 垂直),则古树
垂直),则古树![]() 的高度约为
的高度约为![]() ( )
( )
A.![]() 米B.
米B.![]() 米C.
米C.![]() 米D.
米D.![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在坐标平面内,△ABC的顶点位置如图所示.
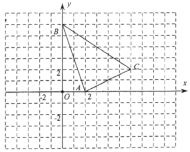
(1)将△ABC作平移交换(x,y)→(x+2,y-3)得到![]() ,画出
,画出![]() .
.
(2)以点O为位似中心缩小![]() 得到
得到![]() ,使
,使![]() 与
与![]() 的相似比为1:2,且点A与其对应点
的相似比为1:2,且点A与其对应点![]() 位于点O的两侧,画出
位于点O的两侧,画出![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A坐标为(-8,0),点B坐标为(0,6),⊙O的半径为4(O为坐标原点),点C是⊙O上一动点,过点B作直线AC的垂线BP,P为垂足.点C在⊙O上运动一周,则点P运动的路径长等于________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+
x2+![]() x﹣4与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
x﹣4与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
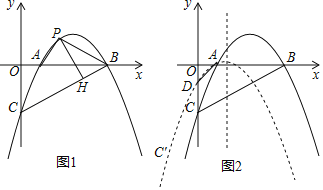
(1)连接BC,P是线段BC上方抛物线上的一动点,过点P作PH⊥BC于点H,当PH长度最大时,在△APB内部有一点M,连接AM、BM、PM,求AM+![]() BM+PM的最小值.
BM+PM的最小值.
(2)若点D是OC的中点,将抛物线y=![]() x2+
x2+![]() x﹣4沿射线AD方向平移
x﹣4沿射线AD方向平移![]() 个单位得到新抛物线y′,C′是抛物线y′上与C对应的点,抛物线y'的对称轴上有一动点N,在平面直角坐标系中是否存在一点S,使得C′、N、B、S为顶点的四边形是矩形?若存在,请直接写出点S的坐标;若不存在,请说明理由.
个单位得到新抛物线y′,C′是抛物线y′上与C对应的点,抛物线y'的对称轴上有一动点N,在平面直角坐标系中是否存在一点S,使得C′、N、B、S为顶点的四边形是矩形?若存在,请直接写出点S的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() 的顶点
的顶点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 边上,高
边上,高![]() 与正方形的边长相等,连接
与正方形的边长相等,连接![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,下列说法:①
,下列说法:①![]() ;②连接
;②连接![]() ,
,![]() ,则
,则![]() 为直角三角形;③
为直角三角形;③![]() ;④若
;④若![]() ,
,![]() ,则
,则![]() 的长为
的长为![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )
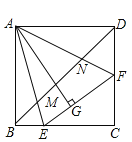
A.4B.3C.2D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com