Question

已知二次函数的图象与轴交于点(，0)、点，

 

与轴交于点．

（1）求点坐标；

（2）点从点出发以每秒1个单位的速度沿线段向点运动，到达点后停止运动，过点作交于点，将四边形沿翻折，得到四边形，设点的运动时间为．

①当为何值时，点恰好落在二次函数图象的对称轴上；

 

②设四边形落在第一象限内的图形面积为，求关于的函数关系式，并求出的最大值．

 

Answer 1

解：（1）将A(，0)代入解得………1分

 

∴函数的解析式为

 

令，解得：

∴B(，0)  ……………………………………………………………………2分

（2）①由解析式可得点

二次函数图象的对称轴方程为

 

△中  ∵

∴

∴，

过点A′作轴于点，则

 

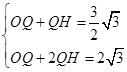∴………………………3分

 

解得

 

则，

∴……………………………………………………4分

②分两种情况：

ⅰ）当时，四边形PQA′C′落在第一象限内的图形为等腰三角形QA’N．

 

 

当时，有最大值S

 

ⅱ）当时，设四边形PQA′C′落在 第一象限内的图形为四边形M O QA′．

   

 

当时，有最大值

 

综上：当时，四边形PQA’ C’落在第一象限内的图形面积有最大值是．

 

解析:略