【题目】在横线上完成下面的证明，并在括号内注明理由．
已知：如图，∠ABC+∠BGD＝180°，∠1＝∠2．
求证：EF∥DB．
证明：∵∠ABC+∠BGD＝180°，（已知）
∴ ．（ ）
∴∠1＝∠3．（ ）
又∵∠1＝∠2，（已知）
∴ ．（ ）
∴EF∥DB．（ ）
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，△ABC在直角坐标系中，
（1）请写出△ABC各点的坐标．
（2）若把△ABC向上平移2个单位，再向左平移1个单位得到△A′B′C′，写出 A′、B′、C′的坐标，并在图中画出平移后图形．
（3）求出三角形ABC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为响应“学雷锋、树新风、做文明中学生”号召，某校开展了志愿者服务活动，活动项目有“戒毒宣传”、“文明交通岗”、“关爱老人”、“义务植树”、“社区服务”等五项，活动期间，随机抽取了部分学生对志愿者服务情况进行调查，结果发现，被调查的每名学生都参与了活动，最少的参与了1项，最多的参与了5项，根据调查结果绘制了如图所示不完整的折线统计图和扇形统计图．
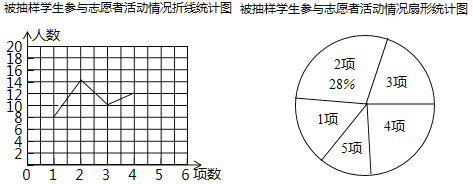
（1）被随机抽取的学生共有多少名？
（2）在扇形统计图中，求活动数为3项的学生所对应的扇形圆心角的度数，并补全折线统计图；
（3）该校共有学生2000人，估计其中参与了4项或5项活动的学生共有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
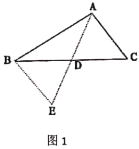
【题目】在△ABC中，∠B＝60°，D、E分别为AB、BC上的点，且AE、CD交于点F．
（1）如图1，若AE、CD为△ABC的角平分线：
①求∠AFD的度数；
②若AD＝3，CE＝2，求AC的长；
（2）如图2，若∠EAC＝∠DCA＝30°，求证：AD＝CE．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，
中
，其中
；
（1）求线段
的长（用
和
的代数式表示）；
（2）如图1，若
，点
在上，点
在
上，点到和BC的距离相等，
，连接
，求
的长；
（3）如图2，若为的中点，，点
分别在线段
上，且
，连接，
和
，求EF的值；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在ABCD中 过点A作AE⊥DC，垂足为E，连接BE，F为BE上一点，且∠AFE=∠D．
（1）求证：△ABF∽△BEC；
（2）若AD=5，AB=8，sinD= 
，求AF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】课外兴趣小组活动时，老师提出了如下问题：
（1）如图1，
中，若
，
，求
边上的中线
的取值范围．小明在组内经过合作交流，得到了如下的解决方法：将
绕点
逆时针旋转
得到
，把
、
、
集中在
中，利用三角形的三边关系可得
，则
；
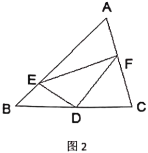
（2）问题解决：受到（1）的启发，请你证明下面命题：如图2，在中，是边上的中点，
，
交于点
，
交于点
，连接
．
①求证：
；
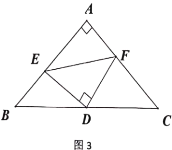
②如图3，若
，探索线段
、
、之间的等量关系，并加以证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
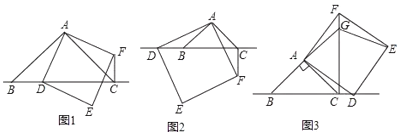
【题目】类比思想就是根据已经学习过的知识，类比探究新知识的思想方法．我们在探究矩形、菱形、正方形等问题中的数量关系时，经常用到类比思想．某数学兴趣小组在数学课外活动中，研究三角形和正方形的性质时，做了如下探究：在
中，
点
为直线
上一动点(点不与
重合)，以
为边在右侧作正方形
连接
．
（1）（观察猜想）如图①，当点在线段上时；
①与的位置关系为： ；
②
之间的数量关系为： ；(将结论直接写在横线上)
（2）（数学思考）如图②，当点在线段
的延长线上时，结论①②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明；
（3）（拓展延伸）如图③，当点在线段的延长线上时，延长
交于点
，连接
．若已知
请直接写出的长．(提示： ．过
作
于
过
作
于
于
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
