
【题目】如图,![]() 中,
中,![]() ,在
,在![]() 上截取
上截取![]() ,
,![]() 为
为![]() 上一点,且
上一点,且![]() ,过点
,过点![]() 作
作![]() 的垂线,分别交
的垂线,分别交![]() 、
、![]() 于
于![]() 、
、![]() ,连接
,连接![]() 交
交![]() 于
于![]() 。
。
(1)若![]() 为
为![]() 的中点,
的中点,![]() ,求
,求![]() 的长;
的长;
(2)求证:![]() .
.

【答案】(1)![]() ;(2)解解析.
;(2)解解析.
【解析】
(1)先证明△ABC为等边三角形,得到AB=BD=4,进而求得BE=2,在Rt△EBF中,∠EBF=60°,得到∠BEF=30°,求出BF=![]() BE=1.再利用勾股定理即可解答;
BE=1.再利用勾股定理即可解答;
(2)取FM=BF,由EF⊥BM,BF=FM,知BE=EM=CD,再证明△EMH≌△CDH,得到DH=HM,从而FH=FM+MH=BF+DH=![]() BE+DH.
BE+DH.
(1)∵∠A=60°,AD=AB,
∴△ABC为等边三角形,
∴AB=BD=4,
∵E为AB的中点,
∴BE=2,
在Rt△EBF中,∠EBF=60°,
∴∠BEF=30°
∴BF=![]() BE=1.
BE=1.
∴EF=![]() .
.
(2)如图,取FM=BF,由EF⊥BM,BF=FM,知BE=EM=CD,

又∵∠BEF=∠FEM=30°,
∴∠BEM=∠A=60°,
∴EM∥AC,
∴∠MEH=∠HCD,∠EHM=∠CHD,
在△EMH和△CDH中,
 ,
,
∴△EMH≌△CDH,
∴DH=HM,
∴FH=FM+MH=BF+DH=![]() BE+DH.
BE+DH.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
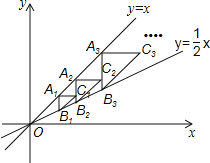
【题目】如图,![]() 点在直线
点在直线![]() 上,过点
上,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,以点
,以点![]() 为直角顶点,
为直角顶点,![]() 为直角边在
为直角边在![]() 的右侧作等腰直角
的右侧作等腰直角![]() ,再过点
,再过点![]() 作
作![]() 轴,分别交直线
轴,分别交直线![]() 和
和![]() 于
于![]() 两点,以点
两点,以点![]() 为直角项点,
为直角项点,![]() 为直角边在
为直角边在![]() 的右侧作等腰直角
的右侧作等腰直角![]() …,按此规律进行下去,则等腰直角
…,按此规律进行下去,则等腰直角![]() 的面积为___. (用含正整数
的面积为___. (用含正整数![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 网格中,每个小正方形的边长都为
网格中,每个小正方形的边长都为![]() .
.
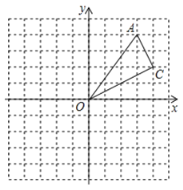
(1)建立如图所示的平面直角坐标系,若点![]() ,则点
,则点![]() 的坐标_______________;
的坐标_______________;
(2)将![]() 向左平移
向左平移![]() 个单位,向上平移
个单位,向上平移![]() 个单位,则点
个单位,则点![]() 的坐标变为_____________;
的坐标变为_____________;
(3)若将![]() 的三个顶点的横纵坐标都乘以
的三个顶点的横纵坐标都乘以![]() ,请画出
,请画出![]() ;
;
(4)图中格点![]() 的面积是_________________;
的面积是_________________;
(5)在![]() 轴上找一点
轴上找一点![]() ,使得
,使得![]() 最小,请画出点
最小,请画出点![]() 的位置,并直接写出
的位置,并直接写出![]() 的最小值是______________.
的最小值是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=9,AC=6,BC=12,点M在AB边上,且AM=3,过点M作直线MN与AC边交于点N,使截得的三角形与原三角形相似,则MN=__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,矩形
,矩形![]() 的一边落在矩形
的一边落在矩形![]() 的一边上,并且矩形
的一边上,并且矩形![]() ,其相似比为
,其相似比为![]() ,连接
,连接![]() 、
、![]() .
.

![]() 试探究
试探究![]() 、
、![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
![]() 将矩形
将矩形![]() 绕着点
绕着点![]() 按顺时针(或逆时针)旋转任意角度
按顺时针(或逆时针)旋转任意角度![]() ,得到图形
,得到图形![]() 、图形
、图形![]() ,请你通过观察、分析、判断
,请你通过观察、分析、判断![]() 中得到的结论是否能成立,并选取图
中得到的结论是否能成立,并选取图![]() 证明你的判断;
证明你的判断;
![]() 在
在![]() 中,矩形
中,矩形![]() 绕着点
绕着点![]() 旋转过程中,连接
旋转过程中,连接![]() 、
、![]() 、
、![]() ,且
,且![]()
![]() ,
,![]() ,
,![]() 的面积是否存在最大值或最小值?若存在,求出最大值或最小值;若不存在,请说明理由.
的面积是否存在最大值或最小值?若存在,求出最大值或最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强校园文化建设,某校准备打造校园文化墙,需用甲、乙两种石材经市场调查,甲种石材的费用![]() (元)与使用面积
(元)与使用面积![]()
![]() 间的函数关系如图所示,乙种石材的价格为每平方米
间的函数关系如图所示,乙种石材的价格为每平方米![]() 元.
元.

(1)求![]() 与
与![]() 间的函数解析式;
间的函数解析式;
(2)若校园文化墙总面积共![]() ,其中使用甲石材
,其中使用甲石材![]()
![]() ,设购买两种石材的总费用为
,设购买两种石材的总费用为![]() 元,请直接写出
元,请直接写出![]() 与
与![]() 间的函数解析式;
间的函数解析式;
(3)在(2)的前提下,若甲种石材使用面积多于![]() ,且不超过乙种石材面积的
,且不超过乙种石材面积的![]() 倍,那么应该怎样分配甲、乙两种石材的面积才能使总费用最少?最少总费用为多少元?
倍,那么应该怎样分配甲、乙两种石材的面积才能使总费用最少?最少总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中国制造”是世界上认知度最高的标签之一,因此,我县越来越多的群众选择购买国产空调,已知购买1台A型号的空调比1台B型号的空调少200元,购买2台A型号的空调与3台B型号的空调共需11200元,求A、B两种型号的空调的购买价各是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com