
【题目】已知![]() 的三条边长分别为6,8,12,过
的三条边长分别为6,8,12,过![]() 任一顶点画一条直线,将
任一顶点画一条直线,将![]() 分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画( )
分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画( )
A.6条B.7条C.8条D.9条
【答案】B
【解析】
不妨设AB=6,AC=8,BC=12,分别作三边的垂直平分线,则可得三条,再分以AB、AC为腰和底进行讨论,可得出结论.
解:不妨设AB=6,AC=8,BC=12,分别作三边的垂直平分线,
如图1,则BD=AD,EA=EC,FB=FC,可知AE、BF、AD满足条件;
当AB为腰时,以点A为圆心,AB为半径画圆,分别交BC、AC于点G、H,
以B为圆心,AB为半径,交BC于点J,如图2,则AB=AG,AB=AH,BA=BJ,满足条件;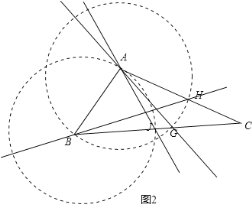
当AC为腰时,如图3,以点C为圆心,CA为半径画圆,交BC于点M,则CA=CM,满足条件;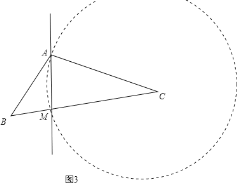
当A为圆心AC为半径画圆时,与AB、BC都没有交点,
因为BC为最长的边,所以不可能存在以BC为腰的等腰三角形,
综上可知满足条件的直线共有7条.
故选B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,平行四边形ABCD中,M、N分别为AB和CD的中点.
(1)求证:四边形AMCN是平行四边形;
(2)当AC、BC满足怎样的数量关系时,四边形AMCN是矩形,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点D的坐标是(﹣3,1),点A的坐标是(4,3).
(1)点B和点C的坐标分别是______、______.
(2)将△ABC平移后使点C与点D重合,点A、B与点E、F重合,画出△DEF.并直接写出E、F的坐标.
(3)若AB上的点M坐标为(x,y),则平移后的对应点M′的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小莹用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,BC为10cm.当小莹折叠时,顶点D落在BC边上的点F处(折痕为AE).

求(1)BF的长;
(2)EF的长 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某品牌太阳能热水器的实物图和横断面示意图,已知真空集热管AB与支架CD所在直线相交于水箱横断面⊙O的圆心O,支架CD与水平面AE垂直,AB=150厘米,∠BAC=30°,另一根辅助支架DE=40![]() 厘米,∠CED=60°.
厘米,∠CED=60°.
(1)求垂直支架CD的长度;
(2)求水箱半径OD的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与思考;
婆罗摩笈多是一位印度数学家与天文学家,书写了两部关于数学与天文的书籍,他的一些数学成就在世界数学史上有较高的地位,他的负数及加减法运算仅晚于中国九章算术而他的负数乘除法法则在全世界都是领先的,他还提出了著名的婆罗摩笈多定理,该定理的内容及证明如下:
已知:如图,四边形ABCD内接与圆O对角线AC⊥BD于点M,ME⊥BC于点E,延长EM交CD于F,求证:MF=DF
证明∵AC⊥BD,ME⊥BC
∴∠CBD=∠CME
∵∠CBD=∠CAD,∠CME=∠AMF
∴∠CAD=∠AMF
∴AF=MF
∵∠AMD=90°,同时∠MAD+∠MDA=90°
∴∠FMD=∠FDM
∴MF=DF,即F是AD中点.
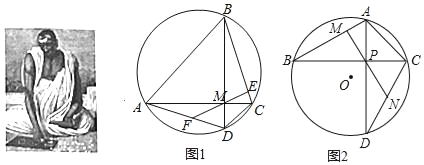
(1)请你阅读婆罗摩笈多定理的证明过程,完成婆罗摩笈多逆定理的证明:
已知:如图1,四边形ABCD内接与圆O,对角线AC⊥BD于点M,F是AD中点,连接FM并延长交BC于点E,求证:ME⊥BC
(2)已知如图2,△ABC内接于圆O,∠B=30°∠ACB=45°,AB=2,点D在圆O上,∠BCD=60°,连接AD 交BC于点P,作ON⊥CD于点N,延长NP交AB于点M,求证PM⊥BA并求PN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】各地“广场舞”噪音干扰的问题备受关注,相关人员对本地区15~65岁年龄段的500名市民进行了随机调查,在调查过程中对“广场舞”噪音干扰的态度有以下五种:A.没影响;B.影响不大;C.有影响,建议做无声运动;D.影响很大,建议取缔;E.不关心这个问题,将调查结果统计整理并绘制成如下两幅不完整的统计图.
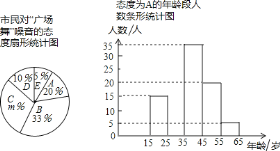
请根据以上信息解答下列问题:
(1)填空m=________,态度为C所对应的圆心角的度数为________;
(2)补全条形统计图;
(3)若全区15~65岁年龄段有20万人,估计该地区对“广场舞”噪音干扰的态度为B的市民人数;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 三点在数轴上,点
三点在数轴上,点![]() 表示的数是
表示的数是![]() ,从点
,从点![]() 出发向右平移7个单位长度得到点
出发向右平移7个单位长度得到点![]() 。
。
(1)求出点![]() 表示的数,画一条数轴并在数轴上标出点
表示的数,画一条数轴并在数轴上标出点![]() 和点
和点![]() ;
;
(2)若此数轴在一张纸上,将纸沿某一条直线对折,此时![]() 点与表示数
点与表示数![]() 的点刚好重合,折痕与数轴有一个交点
的点刚好重合,折痕与数轴有一个交点![]() ,求点
,求点![]() 表示的数的相反数(原卷无此问);
表示的数的相反数(原卷无此问);
(3)在数轴上有一点![]() ,点
,点![]() 到点
到点![]() 和点
和点![]() 的距离之和为11,求点
的距离之和为11,求点![]() 所表示的数;
所表示的数;
(4)![]() 从初始位置分别以1单位长度
从初始位置分别以1单位长度![]() 和2单位长度
和2单位长度![]() 的速度同时向左运动,是否存在
的速度同时向左运动,是否存在![]() 的值,使
的值,使![]() 秒后点
秒后点![]() 到
到![]() 的距离与点
的距离与点![]() 到原点距离相等?若存在请求出
到原点距离相等?若存在请求出![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com