
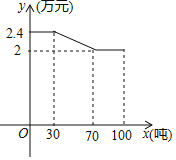
����Ŀ��ij�ػ�����Ӧ�������Ӵ��ҵ��ƶ���ȵĺ��٣�����������ݮ���������磬�����ƶ������ֲ��ݮ�ļ���ָ����ͳһ���ۣ�����������ֺ죮���г����з��֣���ݮ���۵���![]() ����Ԫ�������x���֣�֮��Ĺ�ϵ��ͼ��ʾ
����Ԫ�������x���֣�֮��Ĺ�ϵ��ͼ��ʾ![]() ����֪��ݮ�IJ���Ͷ���ܳɱ�
����֪��ݮ�IJ���Ͷ���ܳɱ�![]() ����Ԫ�������x
����Ԫ�������x![]() ���֣�֮������
���֣�֮������![]() ��
��
��1��ֱ��д����ݮ���۵���![]() ����Ԫ�������
����Ԫ�������![]() ���֣�֮��ĺ�����ϵʽ��
���֣�֮��ĺ�����ϵʽ��
��2����ú�������������![]() ����Ԫ�������
����Ԫ�������![]() ���֣�֮��ĺ�����ϵʽ��
���֣�֮��ĺ�����ϵʽ��
��3��Ϊ���ũ����ֲ��ݮ�Ļ����ԣ������������![]() ��Ԫ/�ֵı�������ƶ������ֲ����Ϊȷ����������������
��Ԫ/�ֵı�������ƶ������ֲ����Ϊȷ����������������![]() ����Ԫ��������
����Ԫ��������![]() ��Ԫ����������Ҫ�ﵽ���ٶ֣�
��Ԫ����������Ҫ�ﵽ���ٶ֣�
���𰸡���1��![]()
![]() ����2��
����2��![]() ����3����������Ҫ�ﵽ
����3����������Ҫ�ﵽ![]() �֣�
�֣�
��������
��1����0��x��30��30��x��70��70��x��100����������ϵʽ��ȷ����2�����ô���ϵ���������ʽ��
��2������w��yx��p�ͣ�1����y��x�Ĺ�ϵʽ�õ�w��x�Ĺ�ϵʽ��
��3���ѣ�2���и����е�w�ֱ��ȥ0.3x�õ�w����x�Ĺ�ϵʽ��Ȼ�����һ�κ��������ʺͶ��κ�����������⣮
�⣺��1����![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ����
ʱ����![]() ��
��
��![]() ��
��![]() �����
�����![]() �����
�����![]() ��
��
![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
![]() ��
��![]() ʱ��
ʱ��![]() ��
��
![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
![]() ��
��![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() �����ֵΪ
�����ֵΪ![]() ���������⣻
���������⣻
��![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() �����ֵΪ
�����ֵΪ![]() ���������⣻
���������⣻
��![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() �����ֵΪ
�����ֵΪ![]() ����ʱ
����ʱ![]() �����
�����![]() ��
��
���Բ�������Ҫ�ﵽ![]() �֣�
�֣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
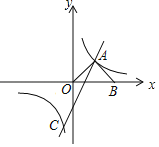
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y1=2x��2��˫����y2=![]() ����A��C���㣬AB��OA��x���ڵ�B����OA=AB��
����A��C���㣬AB��OA��x���ڵ�B����OA=AB��
��1����˫���ߵĽ���ʽ��
��2�����C�����꣬��ֱ��д��y1��y2ʱx��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������������У�ÿ��С�����εı߳�����һ����λ���ȣ���ƽ��ֱ������ϵ�ڣ���ABC��������������ֱ�ΪA��1��4����B��1��1����C��3��1����
��1��������ABC����x��ԳƵġ�A1B1C1��
��2��������ABC�Ƶ�O��ʱ����ת90����ġ�A2B2C2��
��3���ڣ�2���������£����߶�BCɨ�����������������У���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
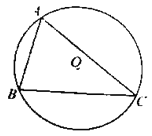
����Ŀ����ͼ����OΪ�����ABC�����Բ���뾶Ϊ5.
��1���ó߹���ͼ������BAC��ƽ���ߣ�����������ӻ�BC�Ľ���E(������ͼ�ۼ�����д����)��
��2������1���еĵ�E����BC�ľ���Ϊ3������CE�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
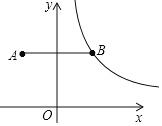
����Ŀ����ƽ��ֱ������ϵ�У���A��-2��3������y��ĶԳƵ�Ϊ��B������AB������������y=![]() ��x��0����ͼ����B������B��BC��x���ڵ�C����P�Ǹ÷���������ͼ��������һ�㣮
��x��0����ͼ����B������B��BC��x���ڵ�C����P�Ǹ÷���������ͼ��������һ�㣮
��1����k��ֵ��
��2������ABP���������2�����P���꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����л�����ʡ��̫ԭ��һ����ںӴ���(��ͼ1)����������߶Ȳ�ͬ���羶Ҳ��ͬ���������ֹ�ͨ�����ţ�������������������ߵĸֹ���ͼ2��ʾ���˸ֹ�(���ƿ��ɶ��κ�����ͼ��-������)��ͬһ��ֱƽ���ڣ��빰�����ڵ�ˮƽ���ཻ��A��B���㣬����Ϊ78��(����ߵ�O��AB�ľ���Ϊ78��)���羶Ϊ90��(��AB=90��)������ߵ�OΪ����ԭ�㣬��ƽ����AB��ֱ��Ϊ![]() �Ὠ��ƽ��ֱ������ϵ����������߸ֹ��ĺ�������ʽΪ( )
�Ὠ��ƽ��ֱ������ϵ����������߸ֹ��ĺ�������ʽΪ( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����б�µĶ�����һ����AB��B��CD���е㣬CD��ˮƽ�ģ�������������£���ӰDE���������ϣ���֪����������CD��12 m����Ӱ��DE��24 m��С����С�������߶���1.6 m��ͬһʱ�̣�С��վ�ڵ�E����Ӱ���������ϣ�С��վ��ƽ���ϣ�Ӱ��Ҳ��ƽ���ϣ����˵�Ӱ���ֱ�Ϊ2 m��1 m����ô����ABΪ________ m.
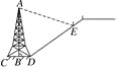
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() �Ƕ��㣬�߳�Ϊ4��
�Ƕ��㣬�߳�Ϊ4��![]() �������н�����ȷ���м����� ��
�������н�����ȷ���м����� ��
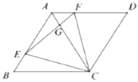
��![]() �� ��
�� ��![]() Ϊ�ȱ�������
Ϊ�ȱ�������
��![]() ����
����![]() ����
����![]()
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��������
��������![]() ����
����![]() ����.
����.
��1����������κ����ı���ʽ��
��2����![]() ��ֱ��
��ֱ��![]() �Ϸ���������һ�㣻
�Ϸ���������һ�㣻
�ٵ�![]() ��������ʱ�����
��������ʱ�����![]() �����ꣻ
�����ꣻ
���ڢٵ������£���![]() ���������߶Գ���ĶԳƵ�Ϊ
���������߶Գ���ĶԳƵ�Ϊ![]() ����ֱ��
����ֱ��![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ��ֱ��
��ʹ��ֱ��![]() ��ֱ��
��ֱ��![]() �ļн���
�ļн���![]() �������������ڣ�ֱ��д����
�������������ڣ�ֱ��д����![]() �����꣬�������ڣ���˵������.
�����꣬�������ڣ���˵������.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com