
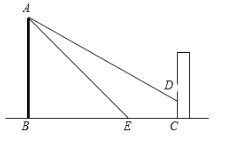
【题目】如图,某公园内有一座古塔AB,在塔的北面有一栋建筑物,某日上午9时太阳光线与水平面的夹角为32°,此时塔在建筑物的墙上留下了高3米的影子CD.中午12时太阳光线与地面的夹角为45°,此时塔尖A在地面上的影子E与墙角C的距离为15米(B、E、C在一条直线上),求塔AB的高度.(结果精确到0.01米)
参考数据:sin32°≈0.5299,cos32°≈0.8480,tan32°≈0.6249,![]() .
.
 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料:
材料一:一个大于1的自然数,除了1和它自身外,不能被其他自然数整除的数叫做质数,否则称为合数.
其中,1和0既不是质数也不是合数.
材料二:一个较大自然数是质数还是合数通常用“![]() 法”来判断,主要分为三个步骤:
法”来判断,主要分为三个步骤:
第一步,找出大于![]() 且最接近
且最接近![]() 的平方数
的平方数![]() ;
;
第二步,用小于![]() 的所有质数去除
的所有质数去除![]() ;
;
第三步,如果这些质数都不能整除![]() ,那么
,那么![]() 是质数;如果这些质数中至少有一个能整除
是质数;如果这些质数中至少有一个能整除![]() ,那么
,那么![]() 就是合数.
就是合数.
如何判断239是质数还是合数?
第一步,![]() ;
;
第二步,小于16的质数有:2、3、5、7、11、13,用2、3、5、7、11、13依次去除239;
第三步,发现没有质数能整除239,所以239是质数.
材料三:分解质因数就是把一个合数分解成若干个质数的乘积的形式,通过分解质因数可以确定该合数的约数的个数.若![]() …(
…(![]() ,
,![]() ,
,![]() …是不相等的质数,
…是不相等的质数,![]() ,
,![]() ,
,![]() …是正整数),则合数
…是正整数),则合数![]() 共有
共有![]() …个约数.如
…个约数.如![]() ,
,![]() ,则8共有4个约数;又如
,则8共有4个约数;又如![]() ,
,![]() ,则12共有6个约数.请用以上方法解决下列问题:
,则12共有6个约数.请用以上方法解决下列问题:
(1)请用“![]() 法”判断163是质数还是合数;
法”判断163是质数还是合数;
(2)求有12个约数的最小自然数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某同学家的一面窗户上安装有遮阳篷,图2和图3是截面示意图,CD是遮阳篷,窗户AB为1.5米,BC为0.5米.该遮阳篷有伸缩功能.如图2,该同学在夏季某日的正午时刻测得太阳光和水平线的夹角为60°,遮阳篷CD正好将进入窗户AB的阳光挡住;如图3,该同学在冬季某日的正午时刻测得太阳光和水平线的夹角为30°,将遮阳篷收缩成CD′时,遮阳篷正好完全不挡进入窗户AB的阳光.
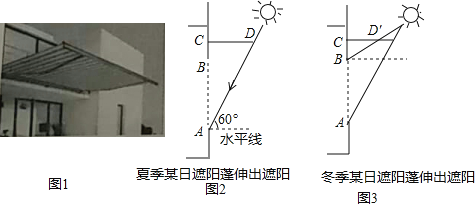
(1)计算图3中CD′的长度比图2中CD的长度收缩了多少米;(结果保留根号)
(2)如果图3中遮阳篷的长度为图2中CD的长度,请计算该遮阳篷落在窗户AB上的阴影长度为多少米?(请在图3中画图并标出相应字母,然后再计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:若抛物线![]() 的顶点
的顶点![]() 在抛物线
在抛物线![]() 上,抛物线
上,抛物线![]() 的顶点
的顶点![]() 也在抛物线
也在抛物线![]() 上(点
上(点![]() 与点
与点![]() 不重合),我们称这样的两条抛物线
不重合),我们称这样的两条抛物线![]() 、
、![]() 互为“友好”抛物线,如图1.
互为“友好”抛物线,如图1.
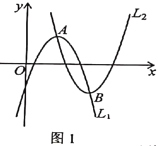
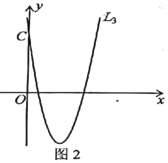
解决问题:如图2,已知物线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)若点![]() 与点
与点![]() 关于抛物线
关于抛物线![]() 的对称轴对称,求点
的对称轴对称,求点![]() 的坐标;
的坐标;
(2)求出以点![]() 为顶点的
为顶点的![]() 的“友好”抛物线
的“友好”抛物线![]() 的解析式;
的解析式;
(3)直接写出![]() 与
与![]() 中
中![]() 同时随
同时随![]() 增大而增大的自变量
增大而增大的自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在图(1)中,在![]() 中,
中,![]() ,垂足为点
,垂足为点![]() ,点
,点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿射线
的速度沿射线![]() 运动,当点
运动,当点![]() 与点
与点![]() 重合时,运动停止.过点
重合时,运动停止.过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() 在射线
在射线![]() 上的对应点为点
上的对应点为点![]() ,连接
,连接![]() .若
.若![]() 与
与![]() 的重叠部分面积为
的重叠部分面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() ,
,![]() 关于
关于![]() 的函数图象如图(2)所示(其中
的函数图象如图(2)所示(其中![]() ,
,![]() ,
,![]() 时,函数解析式不同).
时,函数解析式不同).
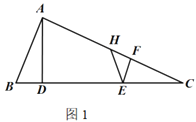
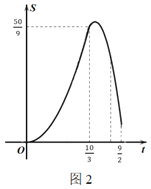
(1)求![]() 的长;
的长;
(2)求![]() 关于
关于![]() 的函数关系式,并写出自变量的取值范围.
的函数关系式,并写出自变量的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() 在反比例函数
在反比例函数![]() 的图象上运动,且始终保持线段
的图象上运动,且始终保持线段![]() 的长度不变.
的长度不变.![]() 为线段
为线段![]() 的中点,连接
的中点,连接![]() .则线段
.则线段![]() 长度的最小值是_____(用含
长度的最小值是_____(用含![]() 的代数式表示).
的代数式表示).
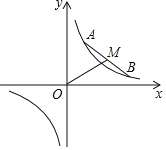
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为![]() 的网格中,
的网格中,![]() 的顶点
的顶点![]() 均在格点上,点
均在格点上,点![]() 在
在![]() 上,且点
上,且点![]() 也在格点上.
也在格点上.
(Ⅰ)![]() 的值为_____________;
的值为_____________;
(Ⅱ)![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的一段圆弧.在如图所示的网格中,将线段
为半径的一段圆弧.在如图所示的网格中,将线段![]() 绕点
绕点![]() 逆时针旋转得到
逆时针旋转得到![]() ,旋转角为,连接
,旋转角为,连接![]() ,
,![]() ,当
,当![]() 的值最小时,请用无刻度的直尺画出点
的值最小时,请用无刻度的直尺画出点![]() ,并简要说明点
,并简要说明点![]() 的位置是如何找到的(不要求证明)______.
的位置是如何找到的(不要求证明)______.
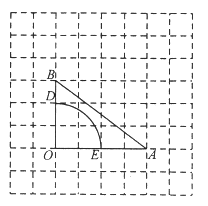
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:若⊙C上存在两个点A、B,使得点P在射线BC上,且∠APB![]() ∠ACB(0°<∠ACB<180°),则称P为⊙C的依附点.
∠ACB(0°<∠ACB<180°),则称P为⊙C的依附点.
(1)当⊙O的半径为1时,
①已知点D(﹣1,0),E(0,﹣2),F(2.5,0),在点D、E、F中,⊙O的依附点是 ;
②点T在直线y=﹣x上,若T为⊙O的依附点,求点T的横坐标t的取值范围;
(2)⊙C的圆心在x轴上,半径为2,直线y=﹣x+2与x轴、y轴分别交于点M、N,若线段MN上的所有点都是⊙C的依附点,直接写出圆心C的横坐标m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】横、纵坐标均为整数的点称为格点,如图,![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() 均为格点,
均为格点,![]() 上的点
上的点![]() 也为格点,用无刻度的直尺作图:
也为格点,用无刻度的直尺作图:
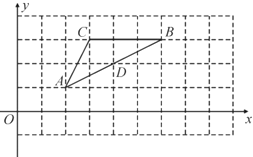
(1)将线段![]() 绕点
绕点![]() 顺时针旋转90°,得到线段
顺时针旋转90°,得到线段![]() ,写出格点
,写出格点![]() 的坐标;
的坐标;
(2)将线段![]() 平移至线段
平移至线段![]() ,使点
,使点![]() 与点
与点![]() 重合,直接写出格点
重合,直接写出格点![]() 的坐标;
的坐标;
(3)画出线段![]() 关于
关于![]() 对称的线段
对称的线段![]() ,保留作图痕迹.
,保留作图痕迹.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com