
【题目】甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
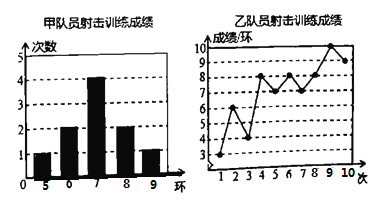
根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 |
|
|
|
|
乙 |
|
|
|
|
(1)写出表格中![]() 的值:
的值:
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
【答案】(1)![]() ,
,![]() ,
,![]() ,
,![]() ;(2)选择乙,理由见解析
;(2)选择乙,理由见解析
【解析】
(1)利用平均数的计算公式直接计算平均分即可;将乙的成绩从小到大重新排列,用中位数的定义直接写出中位数即可;根据乙的平均数利用方差的公式计算即可;
(2)结合平均数和中位数、众数、方差三方面的特点进行分析.
解:(1)甲的平均成绩![]() (环),
(环),
∵乙射击的成绩从小到大从新排列为:3、4、6、7、7、8、8、8、9、10,
∴乙射击成绩的中位数![]() (环),
(环),
又∵乙射击的成绩从小到大从新排列为:3、4、6、7、7、8、8、8、9、10,
∴乙射击成绩的众数:c=8(环)
其方差为:
![]()
=![]() ×(16+9+1+0+3+4+9)
×(16+9+1+0+3+4+9)
=![]()
=![]() ;
;
(2)从平均成绩看甲、乙二人的成绩相等均为7环,从中位数看甲射中7环以上的次数小于乙,从众数看甲射中7环的次数最多而乙射中8环的次数最多,从方差看甲的成绩比乙的成绩稳定,
综合以上各因素,若选派一名学生参加比赛的话,可选择乙参赛,因为乙获得高分的可能更大.


科目:初中数学 来源: 题型:
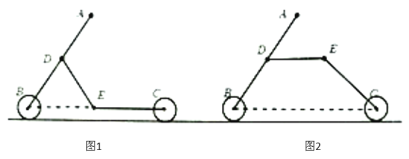
【题目】某工厂生产某种多功能儿童车,根据需要可变形为图1的滑板车或图2的自行车,已知前后车轮半径相同,![]() ,
,![]() ,车杆
,车杆![]() 与
与![]() 所成的
所成的![]() ,图1中
,图1中![]() 、
、![]() 、
、![]() 三点共线,图2中的座板
三点共线,图2中的座板![]() 与地面保持平行.问变形前后两轴心
与地面保持平行.问变形前后两轴心![]() 的长度有没有发生变化?若不变,请写出
的长度有没有发生变化?若不变,请写出![]() 的长度;若变化,请求出变化量?(参考数据:
的长度;若变化,请求出变化量?(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
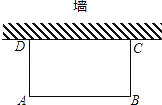
【题目】如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地.
(1)怎样围才能使矩形场地的面积为750m2?
(2)能否使所围矩形场地的面积为810m2 ,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=x2﹣2mx+m2﹣1.
(1)求抛物线顶点C的坐标(用含m的代数式表示);
(2)已知点A(0,3),B(2,3),若该抛物线与线段AB有公共点,结合函数图象,求出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和
和![]() ,与
,与![]() 轴交于点
轴交于点![]() 顶点为
顶点为![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 求
求![]() 的度数;
的度数;
![]() 若点
若点![]() 是线段
是线段![]() 上一个动点,过
上一个动点,过![]() 作
作![]() 轴交抛物线于点
轴交抛物线于点![]() ,交
,交![]() 轴于点
轴于点![]() ,设
,设![]() 点的横坐标为
点的横坐标为![]() .
.
①求线段![]() 的最大值;
的最大值;
②若![]() 是等腰三角形,直接写出
是等腰三角形,直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx(k≠0)经过点(12,﹣5),将直线向上平移m(m>0)个单位,若平移后得到的直线与半径为6的⊙O相交(点O为坐标原点),则m的取值范围为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转一个角度,使点O的对应点D落在弧![]() 上.点B的对应点为C.连接BC.则BC的长度是( )
上.点B的对应点为C.连接BC.则BC的长度是( )

A.4B.![]() C.2
C.2![]() D.3
D.3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,E是AB边上的一个动点(不与点A、B重合),连接DE,过点E作EP⊥DE.
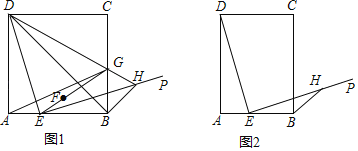
(1)如图1,当四边形ABCD是正方形时,点A关于直线DE的对称点为点F,连接EF并延长交BC于点G;射线DG交EP于点H,连接BH.
①求证:GF=GC
②请求出![]() 的值;
的值;
(2)如图2,四边形ABCD是矩形,且AD=kAB,点H是射线EP上的一点,连接BH,当DE=kEH时,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
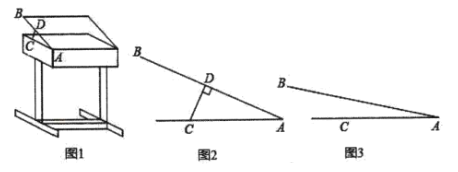
【题目】某课桌生产厂家研究发现,倾斜12°至24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度得桌面.新桌面的设计图如图1,![]() 可绕点
可绕点![]() 旋转,在点
旋转,在点![]() 处安装一根长度一定且
处安装一根长度一定且![]() 处固定,可旋转的支撑臂
处固定,可旋转的支撑臂![]() ,
,![]() .
.
(1)如图2,当![]() 时,
时,![]() ,求支撑臂
,求支撑臂![]() 的长;
的长;
(2)如图3,当![]() 时,求
时,求![]() 的长.(结果保留根号)
的长.(结果保留根号)
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com