练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知甲沿周长为300米的环形跑道按逆时针方向跑步，速度为a米/秒，与此同时在甲后面100米的乙也沿该环形跑道按逆时针方向跑步，速度为3米/秒．

    (1)若a＝1，求甲、乙两人第一次相遇所用的时间；

    (2)若a＞3，甲、乙两人第一次相遇所用的时间为80秒，试求a的值．

    【答案】(1) 50秒;(2) 5.5.

    【解析】

    （1）根据时间=路程差÷速度差，列出算式计算即可求解；
    （2）根据甲的路程-乙的路程=300-100，列出方程计算即可求解．

    (1)设甲、乙两人第一次相遇所用的时间为x秒，根据题意，得：

    3x－x＝100

    解这个方程，得：x＝50．

    答：设甲、乙两人第一次相遇所用的时间为50秒．

    (2)根据题意，得：

    80a－80×3＝300－100

    解这个方程，得：a＝5.5．

    答：的值为5.5．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，点D是BC的中点，DE垂直平分AC，垂足为E，F是BA的中点．求证：DF是AB的垂直平分线．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料： 由于发展时间早、发展速度快，经过20多年大规模的高速开发建设，北京四环内，甚至五环内可供开发建设的土地资源越来越稀缺，更多的土地供应将集中在五环外，甚至六环外的远郊区县．
    据中国经济网2017年2月报道，来自某市场研究院的最新统计，2016年，剔除了保障房后，在北京新建商品住宅交易量整体上涨之时，北京各区域的新建商品住宅交易量则是有涨有跌．其中，昌平、通州、海淀、朝阳、西城、东城六区下跌，跌幅最大的为朝阳区，新建商品住宅成交量比2015年下降了46.82%．而延庆、密云、怀柔、平谷、门头沟、房山、顺义、大兴、石景山、丰台十区的新建商品住宅成交量表现为上涨，涨幅最大的为顺义区，比2015年上涨了118.80%．另外，从环线成交量的占比数据上，同样可以看出成交日趋郊区化的趋势．根据统计，2008年到2016年，北京全市成交的新建商品住宅中，二环以内的占比逐步从3.0%下降到了0.2%；二、三环之间的占比从5.7%下降到了0.8%；三、四环之间的占比从12.3%下降到了2.3%；四、五环之间的占比从21.9%下降到了4.4%．也就是说，整体成交中位于五环之内的新房占比，从2008年的42.8%下降到了2016年的7.7%，下滑趋势非常明显．由此可见，新房市场的远郊化是北京房地产市场发展的大势所趋．（注：占比，指在总数中所占的比重，常用百分比表示）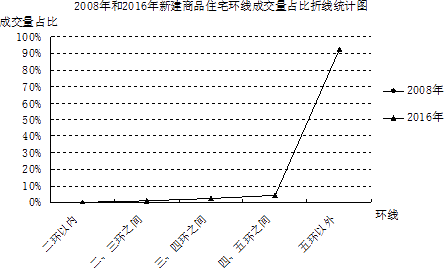

    根据以上材料解答下列问题：
    （1）补全折线统计图；
    （2）根据材料提供的信息，预估 2017年位于北京市五环之内新建商品住宅成交量占比约 ， 你的预估理由是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在边长为5的正方形ABCD中，点E，F分别是BC，DC边上的两个动点（不与点B，C，D重合），且AE⊥EF．

    （1）如图1，当BE=2时，求FC的长；
    （2）延长EF交正方形ABCD外角平分线CP于点P．
    ①依题意将图2补全；
    ②小京通过观察、实验提出猜想：在点E运动的过程中，始终有AE=PE．小京把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的三种想法：
    想法1：在AB上截取AG=EC，连接EG，要证AE=PE，需证△AGE≌△ECP．
    想法2：作点A关于BC的对称点H，连接BH，CH，EH．要证AE=PE，需证△EHP为等腰三角形．
    想法3：将线段BE绕点B顺时针旋转90°，得到线段BM，连接CM，EM，要证AE=PE，需证四边形MCPE为平行四边形．
    请你参考上面的想法，帮助小京证明AE=PE．（一种方法即可）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】图1是某娱乐节目中一个游戏环节的录制现场，场地由等边△ADE和正方形ABCD组成，正方形ABCD两条对角线交于点O，在AD的中点P处放置了一台主摄像机．游戏参与者行进的时间为x，与主摄像机的距离为y，若游戏参与者匀速行进，且表示y与x的函数关系式大致如图2所示，则游戏参与者的行进路线可能是（ ）

    A.A→O→D
    B.E→A→C
    C.A→E→D
    D.E→A→B

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△OAB和△OCD中，OA＝OB，OC＝OD，∠AOB＝∠COD＝α，AC、BD交于M

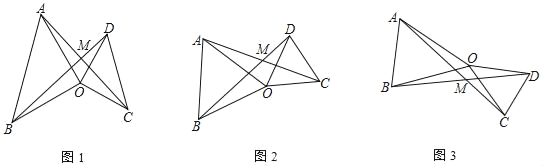
    （1）如图1，当α＝90°时，∠AMD的度数为　 　°

    （2）如图2，当α＝60°时，∠AMD的度数为　 　°

    （3）如图3，当△OCD绕O点任意旋转时，∠AMD与α是否存在着确定的数量关系？如果存在，请你用表示∠AMD，并图3进行证明；若不确定，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料： “共享单车”是指企业与政府合作，在校园、地铁站点、公交站点、居民区、商业区、公共服务区等提供自行车共享的一种服务，是共享经济的一种新形态．共享单车的出现让更多的用户有了更好的代步选择．自行车也代替了一部分公共交通甚至打车的出行．
    Quest Mobile监测的M型与O型单车从2016年10月﹣﹣2017年1月的月度用户使用情况如表所示：

    根据以上材料解答下列问题：
    （1）仔细阅读上表，将O型单车总用户数用折线图表示出来，并在图中标明相应数据；
    （2）根据图表所提提供的数据，选择你所感兴趣的方面，写出一条你发现的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知△ABC是等边三角形，点D是直线BC上一点，以AD为一边在AD的右侧作等边△ADE.

    (1)如图①，点D在线段BC上移动时，直接写出∠BAD和∠CAE的大小关系；

    (2)如图②，点D在线段BC的延长线上移动时，猜想∠DCE的大小是否发生变化．若不变请求出其大小；若变化，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，OD平分∠BOC，OE平分∠AOC．若∠BOC=70°，∠AOC=50°．

    （1）求出∠AOB及其补角的度数；

    （2）请求出∠DOC和∠AOE的度数，并判断∠DOE与∠AOB是否互补，并说明理由.

    查看答案和解析>>

    同步练习册答案