
【题目】如图,在矩形纸片![]() 中,已知
中,已知![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上移动,连接
上移动,连接![]() ,将多边形
,将多边形![]() 沿直线
沿直线![]() 折叠,得到多边形
折叠,得到多边形![]() ,点
,点![]() 、
、![]() 的对应点分别为点
的对应点分别为点![]() 、
、![]() .
.
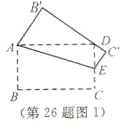
(1)当![]() 恰好经过点
恰好经过点![]() 时(如图1),求线段
时(如图1),求线段![]() 的长;
的长;
(2)若![]() 分别交边
分别交边![]() 、
、![]() 于点
于点![]() 、
、![]() ,且
,且![]() (如图2),求
(如图2),求![]() 的面积;
的面积;
(3)在点![]() 从点
从点![]() 移动到点
移动到点![]() 的过程中,求点
的过程中,求点![]() 运动的路径长.
运动的路径长.

【答案】(1) ![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)根据折叠的性质可得![]() ,
,![]() ,
,![]() ,
,![]() ,根据勾股定理求得
,根据勾股定理求得![]() ,即可得
,即可得![]() ,易证
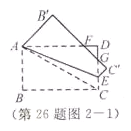
,易证![]() ,根据相似三角形的性质即可求得CE的长;(2)如图2-1,连接AC,根据锐角三角函数求得∠BAC=60°,再求得
,根据相似三角形的性质即可求得CE的长;(2)如图2-1,连接AC,根据锐角三角函数求得∠BAC=60°,再求得![]() ,根据等腰直角三角形的性质求得
,根据等腰直角三角形的性质求得![]() ,即可求得
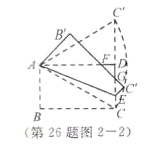
,即可求得![]() 的面积;(3)如图2-2,连接A
的面积;(3)如图2-2,连接A![]() ,则
,则![]() ,点
,点![]() 的运动路径是以点A为圆心,以AC为半径的圆弧,根据弧长公式计算即可.
的运动路径是以点A为圆心,以AC为半径的圆弧,根据弧长公式计算即可.
试题解析:
(1)如图1,由折叠得,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由勾股定理得,![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
又因![]() ,所以
,所以![]()
又![]() ,所以
,所以![]()
所以![]() ,即
,即![]() ,所以
,所以![]()
(2)如图2-1,连接AC,因为∠BAC=![]() ,所以∠BAC=60°,
,所以∠BAC=60°,
故∠DAC=30°,又![]() ,所以
,所以![]() ,
,
由折叠得,![]() ,所以
,所以![]() ,
,
所以![]() ,即
,即![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ;
;
(3) 如图2-2,连接A![]() ,则
,则![]() ,
,
所以点![]() 的运动路径是以点A为圆心,以AC为半径的圆弧;当点E运动到点D时,点
的运动路径是以点A为圆心,以AC为半径的圆弧;当点E运动到点D时,点![]() 恰好在CD的延长线上,此时
恰好在CD的延长线上,此时![]() ,
,
所以点的运动路径长是![]() .
.


科目:初中数学 来源: 题型:
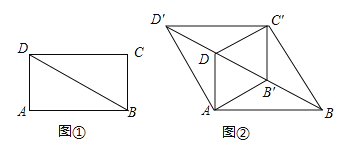
【题目】如图①,BD是矩形ABCD的对角线,∠ABD=30°,AD=1.将△BCD沿射线BD方向平移到△B'C'D'的位置,使B'为BD中点,连接AB',C'D,AD',BC',如图②.
(1)求证:四边形AB'C'D是菱形;
(2)四边形ABC'D′的周长为 ;
(3)将四边形ABC'D'沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出所有可能拼成的矩形周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于M,交AC于N.
(1)若∠ABC=70°,则∠MNA的度数是 .
(2)连接NB,若AB=8cm,△NBC的周长是14cm.
①求BC的长;
②在直线MN上是否存在P,使由P、B、C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强与小刚都住在安康小区,在同一所学校读书.某天早上,小强![]() 从安康小区站乘坐校车去学校,途中需停靠两个站点才能到达学校站点,且每个站点停留
从安康小区站乘坐校车去学校,途中需停靠两个站点才能到达学校站点,且每个站点停留![]() 分钟,校车行驶途中始终保持匀速.当天早上,小刚
分钟,校车行驶途中始终保持匀速.当天早上,小刚![]() 从安康小区站乘坐出租车沿相同路线出发,出租车匀速行驶,比小强乘坐的校车早
从安康小区站乘坐出租车沿相同路线出发,出租车匀速行驶,比小强乘坐的校车早![]() 分钟到学校站点.他们乘坐的车辆从安康小区站出发所行驶路程
分钟到学校站点.他们乘坐的车辆从安康小区站出发所行驶路程![]() (千米)与行驶时间
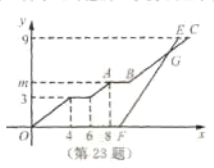
(千米)与行驶时间![]() (分钟)之间的函数图象如图所示.
(分钟)之间的函数图象如图所示.
(1)求点![]() 的纵坐标
的纵坐标![]() 的值;
的值;
(2)小刚乘坐出租车出发后经过多少分钟追到小强所乘坐的校车?并求此时他们距学校站点的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,飞机在一定高度上沿水平直线飞行,先在点![]() 处测得正前方小岛
处测得正前方小岛![]() 的俯角为
的俯角为![]() ,面向小岛方向继续飞行
,面向小岛方向继续飞行![]()
![]() 到达
到达![]() 处,发现小岛在其正后方,此时测得小岛的俯角为
处,发现小岛在其正后方,此时测得小岛的俯角为![]() .如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).
.如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com