
ЁОЬтФПЁПГпЙцзїЭМЪЧжИгУЮоПЬЖШЕФжБГпКЭдВЙцзїЭМЁЃГпЙцзїЭМЪЧЦ№дДгкЙХЯЃРАЕФЪ§бЇПЮЬт.жЛЪЙгУдВЙцКЭжБГпЃЌВЂЧвжЛзМаэЪЙгУгаЯоДЮЃЌРДНтОіВЛЭЌЕФЦНУцМИКЮзїЭМЬт.ГѕжаНзЖЮЭЌбЇУЧЪзДЮНгДЅЕФГпЙцзїЭМЪЧЁАзївЛЬѕЯпЖЮЕШгквбжЊЯпЖЮЁБ.

ЭМ1

ЭМ2
![]()
БИгУЭМ
ЃЈ1ЃЉШчЭМ1ЃЌдкЯпЖЮ![]() ЭтгавЛЕу
ЭтгавЛЕу![]() ЃЌЯждкРћгУГпЙцзїЭМбщжЄЁАСНЕужЎМфЯпЖЮзюЖЬЁБЃЌ
ЃЌЯждкРћгУГпЙцзїЭМбщжЄЁАСНЕужЎМфЯпЖЮзюЖЬЁБЃЌ![]() .ЧыИљОнЬсЪОЃЌгУГпЙцЭъГЩзїЭМЃЌВЂВЙГфбщжЄВНжш.
.ЧыИљОнЬсЪОЃЌгУГпЙцЭъГЩзїЭМЃЌВЂВЙГфбщжЄВНжш.
ЕквЛВНЃЌвд![]() ЮЊдВаФЃЌ
ЮЊдВаФЃЌ![]() ЮЊАыОЖзїЛЁЃЌНЛЯпЖЮ
ЮЊАыОЖзїЛЁЃЌНЛЯпЖЮ![]() гкЕу
гкЕу![]() ЃЌдђ
ЃЌдђ![]() _____________ЃЛ
_____________ЃЛ
ЕкЖўВНЃЌвд![]() ЮЊдВаФЃЌ
ЮЊдВаФЃЌ![]() ЮЊАыОЖзїЛЁЃЌНЛЯпЖЮ
ЮЊАыОЖзїЛЁЃЌНЛЯпЖЮ![]() гкЕу
гкЕу![]() ЃЌдђ
ЃЌдђ![]() _____________ЃЛ
_____________ЃЛ
дђ![]() ______________
______________![]() _______________
_______________![]()
![]() _______________
_______________
ЙЪЃК![]() .
.
ЃЈ2ЃЉШчЭМ2ЃЌдкжБЯп![]() ЩЯЃЌДгзѓЭљгввРДЮгаЫФИіЕу
ЩЯЃЌДгзѓЭљгввРДЮгаЫФИіЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧв
ЃЌЧв![]() ЃЌ
ЃЌ![]() .Яжвд
.Яжвд![]() ЮЊдВаФЃЌАыОЖГЄЮЊ
ЮЊдВаФЃЌАыОЖГЄЮЊ![]() зїдВЃЌгыжБЯп
зїдВЃЌгыжБЯп![]() СНИіНЛЕужагвВрНЛЕуМЧЮЊЕу
СНИіНЛЕужагвВрНЛЕуМЧЮЊЕу![]() .дйвд
.дйвд![]() ЮЊдВаФЃЛЯрЭЌАыОЖГЄ
ЮЊдВаФЃЛЯрЭЌАыОЖГЄ![]() зїдВЃЌгыжБЯп
зїдВЃЌгыжБЯп![]() СНИіНЛЕужазѓВрНЛЕуМЧЮЊЕу
СНИіНЛЕужазѓВрНЛЕуМЧЮЊЕу![]() .Шє
.Шє![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() Ш§ЕужаЃЌгавЛЕуЗжСэЭтСНЕуЫљСЌЯпЖЮжЎБШЮЊ
Ш§ЕужаЃЌгавЛЕуЗжСэЭтСНЕуЫљСЌЯпЖЮжЎБШЮЊ![]() ЃЌЧѓАыОЖ
ЃЌЧѓАыОЖ![]() ЕФГЄ.
ЕФГЄ.
ЁОД№АИЁПЃЈ1ЃЉзїЭММћНтЮіЃЛAMЃЛBNЃЛAM ЃЛ BN ЃЛMNЃЈ2ЃЉ6ЁЂ10ЁЂ![]() ЁЂ34.
ЁЂ34.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнГпЙцзїЭМЕФВНжшАДВНжшНјааВйзїЃЌИљОнЯпЖЮЕФЪ§СПЙиЯЕНјааХаЖЯМДПЩ.
ЃЈ2ЃЉИљОнЬтФПжаЕФЯпЖЮМфЕФЙиЯЕЃЌЗжРрНјааЬжТлЃЌЗжБ№ЮЊЕБPЕудкQЁЂFжЎМфЪБЃЌЕБQЕудкPЁЂFжЎМфЪБЃЌЕБFЕудкPЁЂQжЎМфЪБЃЌЗжБ№ИљОнЯпЖЮМфЕФЪ§СПЙиЯЕЧѓНтМДПЩ.
НтЃКШчЭМЃК

ЃЈ1ЃЉЕквЛВНЃЌвд![]() ЮЊдВаФЃЌ
ЮЊдВаФЃЌ![]() ЮЊАыОЖзїЛЁЃЌНЛЯпЖЮ
ЮЊАыОЖзїЛЁЃЌНЛЯпЖЮ![]() гкЕу
гкЕу![]() ЃЌдђ
ЃЌдђ![]() AMЃЛ
AMЃЛ
ЕкЖўВНЃЌвд![]() ЮЊдВаФЃЌ
ЮЊдВаФЃЌ![]() ЮЊАыОЖзїЛЁЃЌНЛЯпЖЮ
ЮЊАыОЖзїЛЁЃЌНЛЯпЖЮ![]() гкЕу
гкЕу![]() ЃЌдђ
ЃЌдђ![]() BNЃЛ
BNЃЛ
дђ![]() AM
AM![]() BN
BN![]()
![]() MN
MN
ЙЪЃК![]() .
.
ЃЈ2ЃЉ
ЕБPЕудкQFжЎМфЃЌЂйPF=2QPЪБЃЌ
Ёп![]() =4ЃЌ
=4ЃЌ
Ёр![]() ,
,
ЁпOP=r,
Ёр![]() ЃЌ
ЃЌ
ЭЌРэПЩЕУOQ=8-r
ЁрQP=![]()
Ёп![]() ,
,
ЁрPF=8-r+6=14-rЃЌ
2ЃЈ2r-8ЃЉ=14-r,
НтЕУЃКr=6.

ЂкPQ=2PF
Ёп![]() ,
,
ЁрOF=14ЃЌ
ЁпOP=rЃЌ
ЁрPF=14-r,
Ёп![]() ,
,
ЁрOQ=r-8
Ёр![]() ЃЌ
ЃЌ
ЭЌРэ![]()
ЁрQP=8+2ЁСЃЈ8-rЃЉ=24-2r
Ёр24-2r=14-r
НтЕУr=10.
ЕБQЕудкжаМфЪБЃЌМДQF=2PQ

Ёп![]() =4ЃЌ
=4ЃЌ
Ёр![]() ,
,
Ёп![]() ,
,
ЁрPQ=8-2rЃЌ
QF=6+r
6+r=8-2r
Ёрr=![]() .
.
ЕБFЕудкQЁЂPжЎМфЃЌQF=2FPЪБ

Ёп![]() =4ЃЌ
=4ЃЌ
Ёр![]() ,
,
Ёп![]() ,
,
ЁрFP=r-OF=r-14ЃЌ
QF=r+6ЃЌ
Ёрr+6=2ЃЈr-14ЃЉЃЌ
НтЕУr=34
ЙЪД№АИЪЧЃК6ЁЂ10ЁЂ![]() ЁЂ34.
ЁЂ34.


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌАбЁїABCЯШбиxжсЗелЃЌдйЯђгвЦНвЦ3ИіЕЅЮЛЃЌЕУЕНЁїA1B1C1ЃЌАбетСНВНВйзїЙцЖЈЮЊЗвЦБфЛЛЃЌШчЭМЃЌвбжЊЕШБпШ§НЧаЮABCЕФЖЅЕуBЃЌCЕФзјБъЗжБ№ЪЧЃЈ1ЃЌ1ЃЉЃЌЃЈ3ЃЌ1ЃЉЃЎАбЁїABCОЙ§СЌај3ДЮЗвЦБфЛЛЕУЕНЁїA3B3C3ЃЌдђЕуAЕФЖдгІЕуA3ЕФзјБъЪЧЃЈЁЁЁЁЃЉ

A. ЃЈ5ЃЌЉ![]() ЃЉB. ЃЈ8ЃЌ1+
ЃЉB. ЃЈ8ЃЌ1+![]() ЃЉC. ЃЈ11ЃЌЉ1Љ
ЃЉC. ЃЈ11ЃЌЉ1Љ![]() ЃЉD. ЃЈ14ЃЌ1+
ЃЉD. ЃЈ14ЃЌ1+![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЪ§жсЩЯга AЃЌBЃЌCЃЌD ЫФИіећЪ§Еу(МДИїЕуОљБэЪОећЪ§)ЃЌЧв 2ABЃНBCЃН3CDЃЌШє AЃЌD СНЕуЫљБэЪОЕФЪ§ЗжБ№ЪЧ-5 КЭ 6ЃЌШєНЋЪ§жсдкЕу E ДІелЕўЃЌЕу BЃЌD СНЕужиКЯЃЌдђЕу E БэЪОЕФЪ§ЮЊ______.
![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌФГЩчЛсЪЕМљЛюЖЏаЁзщЪЕЕиВтСПСНАЖЛЅЯрЦНааЕФвЛЖЮКгЕФПэЖШЃЌдкКгЕФФЯАЖБпЕуAДІЃЌВтЕУКгЕФББАЖЕуBдкЦфББЦЋЖЋ45ЁуЗНЯђЃЌШЛКѓЯђЮїзп60mЕНДяCЕуЃЌВтЕУЕуBдкЕуCЕФББЦЋЖЋ60ЁуЗНЯђ.

ЃЈ1ЃЉЧѓЁЯCBAЕФЖШЪ§ЃЛ
ЃЈ2ЃЉЧѓГіетЖЮКгЕФПэ.ЃЈНсЙћОЋШЗЕН1mЃЌБИгУЪ§Он ![]() Ёж1.41ЃЌ
Ёж1.41ЃЌ ![]() Ёж1.73ЃЉ
Ёж1.73ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЃЌ
ЃЌ![]() ЦНЗж
ЦНЗж![]() ЃЌ
ЃЌ![]() ЦНЗж
ЦНЗж![]() .
.

ЭМ1 ЭМ2
ЃЈ1ЃЉШчЭМ1ЃЌЕБ![]() дк
дк![]() ФкВПЪБ
ФкВПЪБ
Ђй![]() __________
__________![]() ЃЛЃЈЬю
ЃЛЃЈЬю![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ЂкЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБ![]() дк
дк![]() ЭтВПЪБЃЌЃЈ1ЃЉЬтЂкЕФ
ЭтВПЪБЃЌЃЈ1ЃЉЬтЂкЕФ![]() ЕФЖШЪ§ЪЧЗёБфЛЏЃПЧыЫЕУїРэгЩ.
ЕФЖШЪ§ЪЧЗёБфЛЏЃПЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
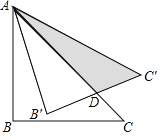
ЁОЬтФПЁПШчЭМЃЌЕШбќжБНЧШ§НЧаЮABCЕФжБНЧБпABЕФГЄЮЊ![]() ЃЌНЋЁїABCШЦЕуAФцЪБеыа§зЊ15ЁуКѓЕУЕНЁїABЁфCЁфЃЌACгыBЁфCЁфЯрНЛгкЕуDЃЌдђЭМжавѕгАЁїADCЁфЕФУцЛ§ЕШгк______ЃЎ
ЃЌНЋЁїABCШЦЕуAФцЪБеыа§зЊ15ЁуКѓЕУЕНЁїABЁфCЁфЃЌACгыBЁфCЁфЯрНЛгкЕуDЃЌдђЭМжавѕгАЁїADCЁфЕФУцЛ§ЕШгк______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпy=kx+bЗжБ№НЛxжсЁЂyжсгкAЃЈ1ЃЌ0ЃЉЁЂBЃЈ0ЃЌЉ1ЃЉЃЌНЛЫЋЧњЯпy=![]() гкЕуCЁЂDЃЎ
гкЕуCЁЂDЃЎ
ЃЈ1ЃЉЧѓkЁЂbЕФжЕЃЛ
ЃЈ2ЃЉаДГіВЛЕШЪНkx+bЃО![]() ЕФНтМЏЃЎ
ЕФНтМЏЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЖдгкЕуPЃЈxЃЌyЃЉЃЌЮвУЧАбЕуPЁфЃЈЉy+1ЃЌx+1ЃЉНазіЕуPЕФАщЫцЕуЃЌвбжЊЕуA1ЕФАщЫцЕуЮЊA2ЃЌЕуA2ЕФАщЫцЕуЮЊA3ЃЌЕуA3ЕФАщЫцЕуЮЊA4ЃЌЁЃЌетбљвРДЮЕУЕНЕуA1ЃЌA2ЃЌA3ЃЌЁЃЌAnЃЎ
ЃЈ1ЃЉШєЕуA1ЕФзјБъЮЊЃЈ2ЃЌ1ЃЉЃЌдђЕуA4ЕФзјБъЮЊ_____ЃЛ
ЃЈ2ЃЉШєЕуA1ЕФзјБъЮЊЃЈaЃЌbЃЉЃЌЖдгкШЮвтЕФе§ећЪ§nЃЌЕуAnОљдкxжсЩЯЗНЃЌдђaЃЌbгІТњзуЕФЬѕМўЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌЁЯAЃН60ЁуЃЌЁЯCЃН40ЁуЃЌDEДЙжБЦНЗжBCЃЌСЌНгBDЃЎ
ЃЈ1ЃЉГпЙцзїЭМЃКЙ§ЕуDзїABЕФДЙЯпЃЌДЙзуЮЊFЃЎЃЈБЃСєзїЭМКлМЃЃЌВЛаДзїЗЈЃЉ
ЃЈ2ЃЉЧѓжЄЃКЕуDЕНBAЃЌBCЕФОрРыЯрЕШЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com