
【题目】旋转变换是解决数学问题中一种重要的思想方法,通过旋转变换可以将分散的条件集中到一起,从而方便解决问题.已知,![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 在边
在边![]() 上,且
上,且![]() .
.

(1)如图![]() ,当
,当![]() 时,将
时,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 到
到![]() 的位置,连接
的位置,连接![]() ,
,
①求![]() 的度数;
的度数;
②求证:![]() ;
;
(2)如图![]() ,当
,当![]() 时,猜想
时,猜想![]() 、
、![]() 、
、![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(3)如图![]() ,当
,当![]() ,
,![]() ,
,![]() 时,请直接写出
时,请直接写出![]() 的长为________.
的长为________.
【答案】(1)①![]() ,②见解析;(2)
,②见解析;(2)![]() ;见解析,(3)
;见解析,(3)![]() .
.
【解析】
(1)①由旋转得,![]() ,
,![]() ,通过求出∠BAD+∠CAE=30°,即可得答案;②通过证明∠DAF=∠DAE,利用SAS即可证明△ADE≌△ADF;(2)如图,将
,通过求出∠BAD+∠CAE=30°,即可得答案;②通过证明∠DAF=∠DAE,利用SAS即可证明△ADE≌△ADF;(2)如图,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 到
到![]() 的位置,连接
的位置,连接![]() 根据等腰直角三角形的性质可得∠C=∠ABC=45°,由旋转的性质可得
根据等腰直角三角形的性质可得∠C=∠ABC=45°,由旋转的性质可得![]() ,
,![]() ,即可证明∠DBF=90°,由(1)可知△ADE≌△ADF,可得DF=DE,根据勾股定理即可得答案;(3)如图,将
,即可证明∠DBF=90°,由(1)可知△ADE≌△ADF,可得DF=DE,根据勾股定理即可得答案;(3)如图,将![]() 绕点
绕点![]() 顺时针旋转120°到△AGB的位置,连接
顺时针旋转120°到△AGB的位置,连接![]() ,过D作DH⊥BG于H,同(2)可得∠GBD=60°,DG=DE,可得∠BDH=30°,利用含30°角的直角三角形的性质可得BH的长,即可得GH的长,利用勾股定理可得DH的长,在Rt△DHG中,利用勾股定理求出DG的长,进而根据△AGD≌△AEC即可得答案.
,过D作DH⊥BG于H,同(2)可得∠GBD=60°,DG=DE,可得∠BDH=30°,利用含30°角的直角三角形的性质可得BH的长,即可得GH的长,利用勾股定理可得DH的长,在Rt△DHG中,利用勾股定理求出DG的长,进而根据△AGD≌△AEC即可得答案.
(1)①由旋转得,![]() ,
,![]() ,
,
∵![]()
∴![]()
②∵∠DAE=30°,∠DAF=30°,
∴∠DAF=∠DAE
在![]() 和
和![]() 中
中

∴![]()
(2)![]()
如图,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 到
到![]() 的位置,连接
的位置,连接![]()
∴![]() ,
,![]()
由(1)得![]()
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]()
∴在![]() 中,
中,![]()
∴![]()

(3)如图,将![]() 绕点
绕点![]() 顺时针旋转120°到△AGB的位置,连接
顺时针旋转120°到△AGB的位置,连接![]() 过D作DH⊥BG于H,
过D作DH⊥BG于H,
∴BG=CE=5,∠C=∠ABG,
∵∠BAC=120°,AB=AC,
∴∠C=∠ABC=30°,
∴∠GBD=∠ABG+∠ABC=30°+30°=60°,
∵DH⊥BG,
∴∠BDH=30°,
∴BH=![]() BD=4×
BD=4×![]() =2,DH=
=2,DH=![]() =
=![]() =2
=2![]() ,
,
∴GH=BG-BH=5-2=3,
由(1)可知△AGD≌△AEC,
∴DG=DE,
在Rt△DHG中,DG=![]() =
=![]() =
=![]() ,
,
∴DE=DG=![]() .
.

故答案为:![]()


科目:初中数学 来源: 题型:
【题目】为创建“美丽乡村”,某村计划购买甲、乙两种树苗共400棵,对本村道路进行绿化改造,已知甲种树苗每棵200元,乙种树苗每棵300元.
![]() 若购买两种树苗的总金额为90000元,求需购买甲、乙两种树苗各多少棵?
若购买两种树苗的总金额为90000元,求需购买甲、乙两种树苗各多少棵?
![]() 若购买甲种树苗的金额不少于购买乙种树苗的金额,则至少应购买甲种树苗多少棵?
若购买甲种树苗的金额不少于购买乙种树苗的金额,则至少应购买甲种树苗多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在扇形OAB中,∠AOB=90°,半径OA=2 ![]() ,将扇形OAB沿过点B的直线折叠,点O恰好落在
,将扇形OAB沿过点B的直线折叠,点O恰好落在 ![]() 上的点D处,折痕交OA于点C,则阴影部分的面积是 .
上的点D处,折痕交OA于点C,则阴影部分的面积是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,过点A引射线AH,交边CD于点H(点H与点D不重合).通过翻折,使点B落在射线AH上的点G处,折痕AE交BC于E,延长EG交CD于F.
(感知)(1)如图①,当点H与点C重合时,猜想FG与FD的数量关系,并说明理由.
(探究)(2)如图②,当点H为边CD上任意一点时,(1)中结论是否仍然成立?请说明理由.
(应用)(3)在图②中,当DF=3,CE=5时,直接利用探究的结论,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某庄有甲、乙两家草莓采摘园的草莓销售价格相同,春节期间,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为![]() (千克),在甲园所需总费用为
(千克),在甲园所需总费用为![]() (元),在乙园所需总费用为
(元),在乙园所需总费用为![]() (元),
(元),![]() 、
、![]() 与
与![]() 之间的函数关系如图所示.
之间的函数关系如图所示.

(1)甲采摘园的门票是_____元,两个采摘园优惠前的草莓单价是每千克____元;
(2)当![]() 时,求
时,求![]() 与
与![]() 的函数表达式;
的函数表达式;
(3)游客在“春节期间”采摘多少千克草莓时,甲、乙两家采摘园的总费用相同.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2AD,点E,F分别是AB,BC边的中点,连接AF,CE交于点M,连接BM并延长交CD于点N,连接DE交AF于点P,则结论:①∠ABN=∠CBN;②DE∥BN;③△CDE是等腰三角形;④EM:BE= ![]() :3;⑤S△EPM=
:3;⑤S△EPM= ![]() S梯形ABCD , 正确的个数有( )
S梯形ABCD , 正确的个数有( )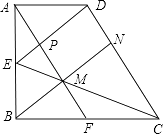
A.5个
B.4个
C.3个
D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=120°,S△ABC=8![]() ,点M,P,N分别是边AB,BC,AC上任意一点,则:
,点M,P,N分别是边AB,BC,AC上任意一点,则:
(1)AB的长为____________.
(2)PM+PN的最小值为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,求:
(1)边AC,AB,BC的长;
(2)点C到AB边的距离;
(3)求△ABC的面积.
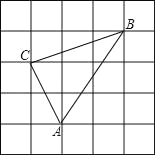
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com