【题目】如图，在□ABCD中，BE平分∠ABC交AD于点E，DF平分∠ADC交BC于点F．
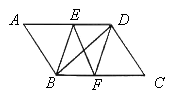
【1】△ABE≌△CDF
【2】若BD⊥EF，则判断四边形EBFD是什么特殊四边形，请证明你的结论．
【答案】
【1】∵四边形
是平行四边，∴
∵
平分
平分
∴
……………3分
∴
…………………………………………4分
【2】由
得
…………………………………5分
在平行四边形中，
∴
∴四边形
是平行四边形…………………………………………7分
若
则四边形是菱形…………………………………8分
【解析】（1）由平行四边形ABCD可得出的条件有：①AB=CD，②∠A=∠C，③∠ABC=∠CDA；已知BE、CD分别是等角∠ABD、∠CDA的平分线，易证得∠ABE=∠CDF④；联立①②④，即可由ASA判定所求的三角形全等；
（2）由（1）的全等三角形，易证得DE=BF，那么DE和BF平行且相等，由此可判定四边形BEDF是平行四边形，根据对角线垂直的平行四边形是菱形即可得出EBFD的形状．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD是边长为1的正方形，E，F为BD所在直线上的两点．若AE=
，∠EAF=135°，则以下结论正确的是（ ）
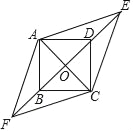
A. DE=1 B. tan∠AFO=
C. AF=
D. 四边形AFCE的面积为
查看答案和解析>>
科目：初中数学 来源： 题型：
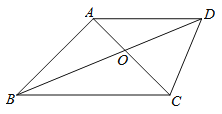
【题目】如图，四边形ABCD中，对角线AC，BD相交于点O，AB=AC=AD，∠DAC=∠ABC．
（1）求证：BD平分∠ABC；
（2）若∠DAC=45°，OA=1，求OC的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知点
在数轴上对应的数为
，点
对应的数为
，且
．
则
________，
________；并将这两个数在数轴上所对应的点，表示出来；
数轴上在点右边有一点
到、两点的距离和为
，若点的数轴上所对应的数为
，求的值；
若点，点同时沿数轴向正方向运动，点运动的速度为
单位/秒，点运动的速度为
单位/秒，若
，求运动时间
的值．
（温馨提示：
、
之间距离记作
，点、在数轴上对应的数分别为
、
，则
．）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为响应承办“绿色奥运”的号召，九年级（1）班全体师生义务植树300棵．原计划每小时植树x棵，但由于参加植树的全体师生植树的积极性高涨，实际工作效率提高为原计划的1.2倍，结果提前20分钟完成任务．则下面所列方程中，正确的是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，AB=AC．D，E是斜边BC上两点，且∠DAE=45°，将△ADC绕点A顺时针旋转90°后，得到△AFB，连接EF，下列结论：
①△AED≌△AEF；
②△ABE∽△ACD；
③BE+DC=DE；
④BE2+DC2=DE2．
其中正确的是（ ）
A．②④ B．①④ C．②③ D．①③
查看答案和解析>>
科目：初中数学 来源： 题型：
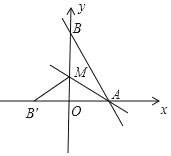
【题目】已知直线y=﹣
x+8与x轴、y轴分别交于点A和点B，M是OB上的一点，若将△ABM沿AM折叠，点B恰好落在x轴上的点B′处，则直线AM的函数解析式是（ ）
A. y=﹣
x+8 B. y=﹣
x+8 C. y=﹣x+3 D. y=﹣x+3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在数轴上，点A、B对应的数分别为a、b，且a、b满足|a+4|+（b﹣8）2＝0．
（1）求A、B所表示的数；
（2）若点C在数轴上对应的数为x，且x是方程2x+1＝
x﹣8的解．
①求线段BC的长；
②在数轴上是否存在点P，使PA+PB＝BC？若存在，求出点P对应的数；若不存在，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
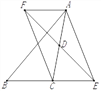
【题目】如图，在△ABC中，D是AC的中点，E是线段BC延长线上一点，过点A作BE的平行线与线段ED的延长线交于点F，连接AE、CF．
(1)求证：AF＝CE；
(2)如果AC＝EF，且∠ACB＝135°，试判断四边形AFCE是什么样的四边形，并证明你的结论
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com