
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.

(1)求证:△DEF是等腰三角形;
(2)当∠A=45°时,求∠DEF的度数.
【答案】(1)见解析;(2)∠DEF=67.5°.
【解析】
(1)由AB=AC,∠ABC=∠ACB,BE=CF,BD=CE.利用边角边定理证明△DBE≌△CEF,然后即可求证△DEF是等腰三角形.
(2)根据∠A=45°可求出∠ABC=∠ACB=67.5°根据△DBE≌△CEF,利用三角形内角和定理即可求出∠DEF的度数.
∵AB=AC,
∴∠ABC=∠ACB,
在△DBE和△CEF中
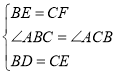 ,
,
∴△DBE≌△CEF,
∴DE=EF,
∴△DEF是等腰三角形;
(2)∵△DBE≌△CEF,
∴∠1=∠3,∠2=∠4,
∵∠A+∠B+∠C=180°,
∴∠B=![]() (180°﹣45°)=67.5°
(180°﹣45°)=67.5°
∴∠1+∠2=112.5°
∴∠3+∠2=112.5°
∴∠DEF=67.5°


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两位同学住在同一小区,学校与小区相距2700米.一天甲从小区步行出发去学校,12分钟后乙也出发,乙先骑公交自行车,途经学校又骑行一段路到达还车点后,立即步行走回学校.已知步行速度甲比乙每分钟快5米,图中的折线表示甲、乙两人之间的距离y(米)与甲步行时间x(分钟)的函数关系图象.则( )

A.乙骑自行车的速度是180米/分B.乙到还车点时,甲,乙两人相距850米
C.自行车还车点距离学校300米D.乙到学校时,甲距离学校200米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从
从![]() 开始沿折线
开始沿折线![]() 以
以![]() 的速度运动,点
的速度运动,点![]() 从
从![]() 开始沿
开始沿![]() 边以
边以![]() 的速度移动,如果点
的速度移动,如果点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,当其中一点到达
同时出发,当其中一点到达![]() 时,另一点也随之停止运动,设运动时间为
时,另一点也随之停止运动,设运动时间为![]() ,当
,当![]() ________时,四边形
________时,四边形![]() 也为矩形.
也为矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在图的半径的活动。小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,求小桥所在圆的半径。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,CD是AB边上的高,若
,CD是AB边上的高,若![]() .
.

(1)求CD的长.
(2)动点P在边AB上从点A出发向点B运动,速度为1个单位/秒;动点Q在边AC上从点A出发向点C运动,速度为v个单位秒![]() ,设运动的时间为
,设运动的时间为![]() ,当点Q到点C时,两个点都停止运动.
,当点Q到点C时,两个点都停止运动.
①若当![]() 时,
时,![]() ,求t的值.
,求t的值.
②若在运动过程中存在某一时刻,使![]() 成立,求v关于t的函数表达式,并写出自变量t的取值范围.
成立,求v关于t的函数表达式,并写出自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工艺美术中,常需设计对称图案.在如图的正方形网格中,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .请在图中再找一个格点
.请在图中再找一个格点![]() ,使它与已知的
,使它与已知的![]() 个格点组成轴对称图形,则点
个格点组成轴对称图形,则点![]() 的坐标为________(如果满足条件的点
的坐标为________(如果满足条件的点![]() 不止一个,请将它们的坐标都写出来).
不止一个,请将它们的坐标都写出来).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,市防汛指挥部决定对某水库的水坝进行加高加固,设计师提供的方案是:水坝加高1米(EF=1米),背水坡AF的坡度i=1∶1,已知AB=3米,∠ABE=120°,求水坝原来的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2).
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=2,求经过点C的反比例函数的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
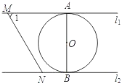
【题目】如图,直线![]() ,
,![]() 与
与![]() 和
和![]() 分别相切于点
分别相切于点![]() 和点
和点![]() .点
.点![]() 和点
和点![]() 分别是
分别是![]() 和
和![]() 上的动点,
上的动点,![]() 沿
沿![]() 和
和![]() 平移.
平移.![]() 的半径为
的半径为![]() ,
,![]() .下列结论错误的是( )
.下列结论错误的是( )
A. ![]() B. 若
B. 若![]() 与
与![]() 相切,则
相切,则![]()
C. 若![]() ,则
,则![]() 与
与![]() 相切 D.
相切 D. ![]() 和
和![]() 的距离为
的距离为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com