
【题目】某校开展“文明在行动”的志愿者活动,准备购买某一品牌书包送到希望学校.在![]() 商店,无论一次购买多少,价格均为每个50元.在
商店,无论一次购买多少,价格均为每个50元.在![]() 商店,一次购买数量不超过10个时,价格为每个60元;一次购买数量超过10个时,超出10个部分打八折.设一次购买该品牌书包的数量为x个.
商店,一次购买数量不超过10个时,价格为每个60元;一次购买数量超过10个时,超出10个部分打八折.设一次购买该品牌书包的数量为x个.
(Ⅰ)根据题意填表:
一次购买数量/个 | 5 | 10 | 15 | … |
| 500 | … | ||
| 600 | … |
(Ⅱ)设在![]() 商店花费
商店花费![]() 元,在
元,在![]() 商店花费
商店花费![]() 元,分别求出
元,分别求出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(Ⅲ)根据题意填空;
①若小丽在![]() 商店和在
商店和在![]() 商店一次购买书包的数量相同,且花费相同,则她在同一商店一次购买书包的数量为______个.
商店一次购买书包的数量相同,且花费相同,则她在同一商店一次购买书包的数量为______个.
②若小丽在同一商店一次购买书包的数量为50个,则她在![]() 两个商店中的______商店购买花费少;
两个商店中的______商店购买花费少;
③若小丽在同一商店一次购买书包花费了1800元,则她在![]() 两个商店中_______商店购买数量多.
两个商店中_______商店购买数量多.
【答案】(1)250,750,300,840;(2)![]() ,
,![]() ;(3)①60;②
;(3)①60;②![]() ;③
;③![]() .
.
【解析】
(1)根据题意列式计算即可;
(2)根据题目中的等量关系即可求出函数表达式;
(3)①根据题意列出方程50x=48x+120,求解即可;
②由题计算出当x=50时,在A店和B店的花费,即可得出答案;
③根据题意求出在A店购买的数量和在B店购买的数量即可得出答案.
(1)x=5时,A:5×50=250,
B:5×60=300,
x=15时,A:15×50=750,
B:10×60+5×60×0.8=840,
故答案为:250,750,300,840;
(2)![]() ;
;
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
即![]() ,
,
综上:![]() ;
;
(3)①50x=48x+120
解得x=60;
②x=50时,
A:50×50=2500,
B:48×50+120=2520
故A花费少;
③50x=1800,
解得:x=36,
48x+120=1800,
解得:x=35,
故A商店购买的数量多.


科目:初中数学 来源: 题型:
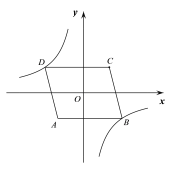
【题目】如图,在平面直角坐标系中,O为□ABCD的对称中心,点A的坐标为(-2,-2),AB=5,AB//x轴,反比例函数y=![]() 的图象经过点D,将□ABCD沿y轴向下平移,使点C的对应点C′落在反比例函数的图象上,则平移过程中线段AC扫过的面积为( )
的图象经过点D,将□ABCD沿y轴向下平移,使点C的对应点C′落在反比例函数的图象上,则平移过程中线段AC扫过的面积为( )
A.10B.18C.20D.24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药店购进一批消毒液,计划每瓶标价100元,由于疫情得到有效控制,药店决定对这批消毒液全部降价销售,设每次降价的百分率相同,经过连续两次降价后,每瓶售价为81元.
(1)求每次降价的百分率.
(2)若按标价出售,每瓶能盈利100%,问第一次降价后销售消毒液100瓶,第二次降价后至少需要销售多少瓶,总利润才能超过5000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
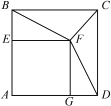
【题目】如图,正方形AEFG的顶点E、G在正方形ABCD的边AB、AD上,连接BF、DF.
![]() (1)求证:BF=DF;
(1)求证:BF=DF;
(2)连接CF,请直接写出![]() 的值为__________(不必写出计算过程).
的值为__________(不必写出计算过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 及一次函数
及一次函数![]() ,将该二次函数在
,将该二次函数在![]() 轴上方的图象沿
轴上方的图象沿![]() 轴翻折到
轴翻折到![]() 轴下方,图象的其余部分不变,得到一个新函数的图象(如图所示),当直线
轴下方,图象的其余部分不变,得到一个新函数的图象(如图所示),当直线![]() 与新函数图象有4个交点时,
与新函数图象有4个交点时,![]() 的取值范围是( )
的取值范围是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
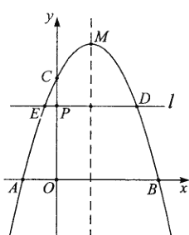
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,
,![]() (点
(点![]() 位于对称轴的左侧),与
位于对称轴的左侧),与![]() 轴交于点
轴交于点![]() .点
.点![]() 为线段
为线段![]() 上一点,过点
上一点,过点![]() 作直线
作直线![]() 轴交图象于点
轴交图象于点![]() ,
,![]() (点
(点![]() 在点
在点![]() 的左侧),且
的左侧),且![]() .
.
(1)求该二次函数的对称轴及![]() 的值.
的值.
(2)将顶点![]() 向右平移
向右平移![]() 个单位至点
个单位至点![]() ,再过点
,再过点![]() 作直线
作直线![]() 的对称点
的对称点![]() ,若点
,若点![]() 在
在![]() 轴上方的图象上一点且到
轴上方的图象上一点且到![]() 轴距离为1,求
轴距离为1,求![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
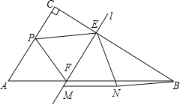
【题目】如图,Rt![]() ABC中,∠C=90°,AC=10,BC=16.动点P以每秒3个单位的速度从点A开始向点C移动,直线l从与AC重合的位置开始,以相同的速度沿CB方向平行移动,且分别与CB,AB边交于E,F两点,点P与直线l同时出发,设运动的时间为t秒,当点P移动到与点C重合时,点P和直线l同时停止运动.在移动过程中,将
ABC中,∠C=90°,AC=10,BC=16.动点P以每秒3个单位的速度从点A开始向点C移动,直线l从与AC重合的位置开始,以相同的速度沿CB方向平行移动,且分别与CB,AB边交于E,F两点,点P与直线l同时出发,设运动的时间为t秒,当点P移动到与点C重合时,点P和直线l同时停止运动.在移动过程中,将![]() PEF绕点E逆时针旋转,使得点P的对应点M落在直线l上,点F的对应点记为点N,连接BN,当BN∥PE时,t的值为_____.
PEF绕点E逆时针旋转,使得点P的对应点M落在直线l上,点F的对应点记为点N,连接BN,当BN∥PE时,t的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
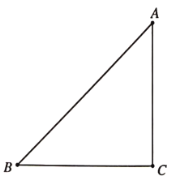
【题目】在等腰直角三角形ABC中,![]() ,P是BC上的一动点(不与B,C重合),射线AP绕点A顺时针旋转
,P是BC上的一动点(不与B,C重合),射线AP绕点A顺时针旋转![]() ,得到射线AQ,过点C作CE垂直AB,交AB与点D,交射线AQ于点E,连接PE.
,得到射线AQ,过点C作CE垂直AB,交AB与点D,交射线AQ于点E,连接PE.
(1)依题意补全图形;
(2)求![]() 的度数;
的度数;
(3)用等式表示线段PE,DE,AC三条线段之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 两地相距
两地相距![]() ,甲、乙两人从两地出发相向而行,甲先出发.图中
,甲、乙两人从两地出发相向而行,甲先出发.图中![]() 表示两人离
表示两人离![]() 地的距离
地的距离![]() 与时间
与时间![]() 的关系,结合图象,下列结论错误的是( )
的关系,结合图象,下列结论错误的是( )
A.![]() 是表示甲离
是表示甲离![]() 地的距离与时间关系的图象
地的距离与时间关系的图象
B.乙的速度是![]()
C.两人相遇时间在![]()
D.当甲到达终点时乙距离终点还有![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com