
����Ŀ����ͼ����C���߶�![]() ��.��P�ӵ�C�������
��.��P�ӵ�C�������![]() �˶����ٶ�Ϊ2cm/s;ͬʱ����QҲ�ӵ�C��4cm/s�ٶȳ�����1s����A��������A��ͣ��2s��Ȼ��ԭ�ٶ����B�˶���.���գ���Q�ȵ�P��1s����B��.���P�˶���ʱ��Ϊt.
�˶����ٶ�Ϊ2cm/s;ͬʱ����QҲ�ӵ�C��4cm/s�ٶȳ�����1s����A��������A��ͣ��2s��Ȼ��ԭ�ٶ����B�˶���.���գ���Q�ȵ�P��1s����B��.���P�˶���ʱ��Ϊt.
(1)�߶�AC�ij�Ϊ cm;��t=3sʱ��P,Q����֮��ľ���Ϊ cm;
(2)���߶�BC�ij�;
(3)��P,Q����ͬʱ��������P�����B�������ʱ���ڣ�tΪ��ֵʱ��P,Q�������1cm��
![]()
���𰸡���1��4��10����2��BC=20�� (3) ![]()
��������
��1�����ݵ�C��4cm/s�ٶȳ�����1s����A�����ɼ�����߶�AC�ij�����t=3sʱ,��Q���ڵ�A�����������CP�ij����ɼ����P,Q����֮��ľ��룻
��2�����P�˶���ʱ��Ϊts�����Q��C�˶���B��ʱ��Ϊ��t-1-1-2-1��s,���������з��̼������t��ֵ��Ȼ�������߶�BC�ij�;
��3�����ݵ�P�͵�O���ٶȣ�����������ϵ�λ�ã���������ۣ����������з��̼������t��ֵ.
�⣺��1���ߵ�C��4cm/s�ٶȳ�����1s����A����
��AC=4��1=4,
���߶�AC�ij�Ϊ4cm��
�ߵ�t=3sʱ,��Q���ڵ�A��,PC=2��3=6,
��PQ=AC+CP=4+6=10,
�� P,Q����֮��ľ���Ϊ10cm.
(2) ���P�˶���ʱ��Ϊts�����Q��C�˶���B��ʱ��Ϊ��t-1-1-2-1��s,���������з��̵ã�2t=4(t-5),
��ã�t=10,
��BC=2��10=20
���߶�BC�ij�Ϊ20cm.
(3) �ٵ���Q��AC��ʱ�����������з��̵ã�4t+2t=1,
��ã�t= ![]() ;
;
�ڵ���Q��BC�����ڵ�P�����ʱ�����������з��̵ã�2t-4(t-4)=1,
��ã�t= ![]() ;
;
�۵���Q��BC�����ڵ�P���Ҳ�ʱ�����������з��̵ã�4(t-4)-2t=1,
��ã�t=![]() ;
;
�ܵ���Q�����B������P��δ����ʱ�����������з��̵ã�20-2t=1,
��ã�t= ![]() ,
,
������������tΪ��ֵΪ![]() ��
��![]() ��
��![]() ��
��![]() ʱ��P,Q�������1cm.
ʱ��P,Q�������1cm.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
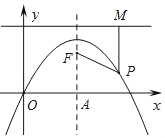
����Ŀ����ͼ��������y=��x2+2x�ĶԳ�����x�ύ�ڵ�A����F�������ߵĶԳ����ϣ��ҵ�F��������Ϊ![]() ������������һ��P��m��n����ֱ��y=
������������һ��P��m��n����ֱ��y=![]() �����ߣ�����ΪM������PF��
�����ߣ�����ΪM������PF��
��1����m=2ʱ����֤��PF=PM��
��2������PΪ������������һ��ʱ��PF=PM�Ƿ������������������֤����������������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
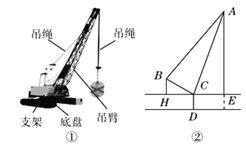
����Ŀ����ͼ�٣��ڷֱ���ij�����ڵ�һ��Ʒʱ��ʵ��ͼ��ʾ��ͼ����֪��������CD�ĸ߶�Ϊ2�ף�֧��BC�ij�Ϊ4�ף���������30���. ����AB��֧��BC�ļн�Ϊ80�㣬����AC������70��ǣ�������ĵ��۶���A�����ĸ߶��Ƕ����ף�����ȷ��0.1��. �ο����ݣ�sin10�㣽cos80���0.17��cos10�㣽sin80���0.98��sin20�㣽cos70���0.34��tan70���2.75��sin70���0.94��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ���ڼ䣬С��һ�ҳ�������ǰ��ij�����Σ��ƻ��ڶ�����������Դ�����Լݳ��Ρ�
 [��
[��
����������Ϣ������������⣺
��1�����ʱ��Ϊ![]() Сʱ�����ü�˾�ij��������Ϊ
Сʱ�����ü�˾�ij��������Ϊ![]() Ԫ�������ҹ�˾�ij��������Ϊ
Ԫ�������ҹ�˾�ij��������Ϊ![]() Ԫ���ֱ����
Ԫ���ֱ����![]() ��
��![]() ����
����![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��2���������С�����㲢ѡ���ĸ����η������㡣
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
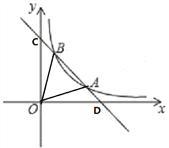
����Ŀ����ͼ��һ�κ���y1=��2x+8��ͼ���뷴��������y2=![]() ��x��0����ͼ����A��3��n����B��m��6�����㣮
��x��0����ͼ����A��3��n����B��m��6�����㣮
��1�����������Ľ���ʽ��
��2�����OAB�������
��3������ͼ��ֱ��д����x��0ʱ��y1��y2���Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
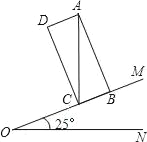
����Ŀ����ͼ����֪��MON=25��������ABCD�ı�BC��OM�ϣ��Խ���AC��ON��
��1�����ACD������
��2����AC=5ʱ����AD�ij������ο����ݣ�sin25��=0.42��cos25��=0.91��tan25��=0.47�������ȷ��0.1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣���ABC����AC=BC����A=30�㣬��D��AB��������ADC=45�㣮
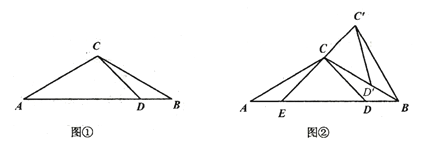
��1������BCD�Ķ�����
��2����ͼ���е���BCD�Ƶ�B˳ʱ����ת���õ���BC��D��������D��ǡ������BC����ʱ����ͼ����ʾ������C��C���ӳ���AB�ڵ�E��
������C��CB�Ķ�����
����֤����C��BD�����CAE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˷ḻѧ���Ŀ�����ijУ��������100�������a��a��10������ë���ģ������鷢�֣��ס�������������Ʒ�̵���ͬ���ļ۸����ͬ��Ʒ�Ƶ��������ë���ģ���֪ÿ�������ÿ����ë���Ĺ�25Ԫ������������������ë���ĵķ���������ȣ���Ǣ̸�����̵���Żݷ����ǣ�ÿ����ʮ��������һ����ë���ģ����̵���Żݷ����ǣ�����������������80����������ë���Ŀɴ���ۣ�
��1����ÿ������xԪ����ÿ����ë����______Ԫ(�ú�x�Ĵ�����ʾ)�������ÿ�������ÿ����ë���ĵļ۸�ֱ��Ƕ��٣�
��2�����ú�a�Ĵ���ʽ�ֱ��ʾ�������̵�����̵깺�������ķ��ã�
��3��������ߣ�����һ���̵깺���㣿��ֱ��д�����ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��װ��˾��С��ҵĴ����������ͼ��ʾ��װ�������Ϸ����ϴ�ü(��Ӱ����)�������뾶��ͬ���ķ�֮һԲ���.
(1)�ֱ�����ʽ��ʾ��ü�ò��ʹ���������.(�����������Բ���).
(2)�۲�(1)�еĽ���������ǵ���ʽ���Ƕ���ʽ�������ֱ��Ƕ��٣�
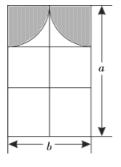
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com