
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 两点(点
两点(点![]() 位于点
位于点![]() 的左侧),与
的左侧),与![]() 轴相交于点
轴相交于点![]() ,
,![]() 是抛物线的顶点,直线
是抛物线的顶点,直线![]() 是抛物线的对称轴,且点
是抛物线的对称轴,且点![]() 的坐标为
的坐标为![]() .
.
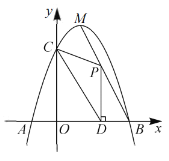
(1)求抛物线的解析式.
(2)已知![]() 为线段
为线段![]() 上一个动点,过点
上一个动点,过点![]() 作
作![]() 轴于点
轴于点![]() .若
.若![]() 的面积为
的面积为![]() .
.
①求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
②当![]() 取得最值时,求点
取得最值时,求点![]() 的坐标.
的坐标.
(3)在(2)的条件下,在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为等腰三角形?如果存在,请求出点
为等腰三角形?如果存在,请求出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②当
;②当![]() 时,
时,![]() 取得最大值
取得最大值![]() ,此时
,此时![]() ;(3)存在,点
;(3)存在,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)点C坐标代入解析式可求c的值,由对称轴可求b的值,即可求解;
(2)①先求出点M,点A,点B的坐标,利用待定系数法可求BM解析式,由三角形的面积公式可求解;
②利用二次函数的性质可求解;
(3)分三种情况讨论,利用两点距离公式列出方程可求解.
(1)![]() 抛物线
抛物线![]() 的对称轴为直线
的对称轴为直线![]() .
.
又![]() 抛物线与
抛物线与![]() 轴的交点为
轴的交点为![]() ,
,
![]() 抛物线的解析式为
抛物线的解析式为![]() .
.
(2)①![]() 顶点
顶点![]() .
.
设直线![]() 的解析式为
的解析式为![]() .
.
将![]() 代入,
代入,
得![]() 解得
解得![]()
![]() 直线
直线![]() 的解析式为
的解析式为![]() .
.
![]() 轴且
轴且![]() ,
,
![]() 的面积
的面积![]() .
.
![]() 点
点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,
![]() ,
,
故![]() 与
与![]() 之间的函数关系式为
之间的函数关系式为![]() .
.
②![]() ,
,
![]() 当
当![]() 时,
时,![]() 取得最大值
取得最大值![]() ;
;
当![]() 时,
时,![]() 没有最小值.
没有最小值.
综上,当![]() 时,
时,![]() 取得最大值
取得最大值![]() ,此时
,此时![]()
(3)存在.
当![]() 时,
时,
![]() ,
,
![]() ,
,
解得![]() (舍去)或
(舍去)或![]() ,此时
,此时![]() .
.
当![]() 时,
时,
![]()
![]()
解得![]() (舍去)或
(舍去)或![]() ,此时
,此时![]() .
.
当![]() 时,
时,
![]() ,
,
![]() ,
,
解得![]() 或
或![]() ,均不符合题意,舍去.
,均不符合题意,舍去.
综上所诉,存在点![]() 使
使![]() 为等腰三角形,点
为等腰三角形,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】某快递公司甲、乙两名快递员7月上旬10天里派送快递,乙比甲晚工作一段时间,工作期间快递员甲因事停工3天,各自的工作效率一定,他们各自的工作量![]() (件)随工作时间
(件)随工作时间![]() (天)变化的图像如图所示.则有下列说法:①甲工人的工作效率为60件/天;②乙工人每天比甲工人少送10件;③甲工人一共送420件;④乙比甲少工作2天.其中正确的个数是( )
(天)变化的图像如图所示.则有下列说法:①甲工人的工作效率为60件/天;②乙工人每天比甲工人少送10件;③甲工人一共送420件;④乙比甲少工作2天.其中正确的个数是( )
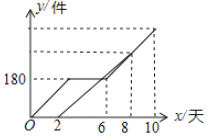
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,把△ABD、△ACD分别以AB、AC为对称轴翻折变换,D点的对称点为E、F,延长EB、FC相交于G点.
(1)求证:四边形AEGF是正方形;
(2)求AD的长.
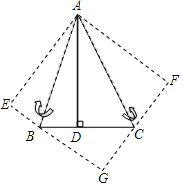
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() 是最大的负整数,且
是最大的负整数,且![]() 满足
满足![]() .
.
![]()
(1)a=________,b=________,c=________.
(2)若将数轴折叠,使得点![]() 与点
与点![]() 重合,则点
重合,则点![]() 与数________表示的点重合;
与数________表示的点重合;
(3)点![]() 开始在数轴上运动,若点
开始在数轴上运动,若点![]() 以每秒1个单位长度的速度向左运动,同时,点
以每秒1个单位长度的速度向左运动,同时,点![]() 和点
和点![]() 分别以每秒2个单位长度和3个单位长度的速度向右运动,假设
分别以每秒2个单位长度和3个单位长度的速度向右运动,假设![]() 秒钟过后,若点
秒钟过后,若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,则
,则![]() ________,
________,![]() ________.(用含
________.(用含![]() 的代数式表示)
的代数式表示)
(4)![]() 的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值。
的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了丰富学生课余生活,开展了“第二课堂”活动,推出了以下四种选修课程:![]() .绘画;
.绘画;![]() .唱歌;
.唱歌;![]() .跳舞;
.跳舞;![]() .演讲;
.演讲;![]() .书法.学校规定:每个学生都必须报名且只能选择其中的一个课程.学校随机抽查了部分学生,对他们选择的课程情况进行了统计,并绘制了如下两幅不完整的统计图.
.书法.学校规定:每个学生都必须报名且只能选择其中的一个课程.学校随机抽查了部分学生,对他们选择的课程情况进行了统计,并绘制了如下两幅不完整的统计图.
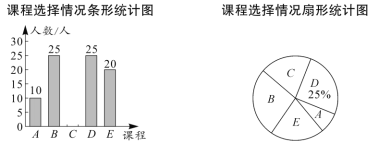
请结合统计图中的信息解决下列问题:
(1)这次抽查的学生人数是多少人?
(2)将条形统计图补充完整.
(3)求扇形统计图中课程![]() 所对应扇形的圆心角的度数.
所对应扇形的圆心角的度数.
(4)如果该校共有1200名学生,请你估计该校选择课程![]() 的学生约有多少人.
的学生约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长均为1的方格纸中,其中端点![]() 、
、![]() 均在小正方形的顶点上.
均在小正方形的顶点上.
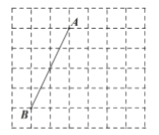
(1)在图中画出平行四边形![]() ,点
,点![]() 和点
和点![]() 均在小正方形的顶点上,且平行四边形
均在小正方形的顶点上,且平行四边形![]() 的面积为12;
的面积为12;
(2)在图中画出以![]() 为腰的等腰直角
为腰的等腰直角![]() ,且点
,且点![]() 在小正方形的顶点上;
在小正方形的顶点上;
(3)连接![]() ,直接写出
,直接写出![]() 的正切值.
的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程.
已知:直线及直线外一点![]() .
.

求作:![]() ,使得
,使得![]() .
.
作法:如图,
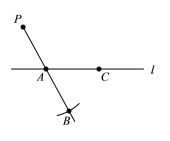
①在直线上取一点![]() ,作射线
,作射线![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交
长为半径画弧,交![]() 的延长线于点
的延长线于点![]() ;
;
②在直线上取一点![]() (不与点
(不与点![]() 重合),作射线
重合),作射线![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交
长为半径画弧,交![]() 的延长线于点
的延长线于点![]() ;
;
③作直线![]() .
.
所以直线![]() 就是所求作的直线.
就是所求作的直线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵![]() _______,
_______,![]() _______,
_______,
∴![]() (____________)(填推理的依据).
(____________)(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生阅读能力,我区某校倡议八年级学生利用双休日加强课外阅读,为了解同学们阅读的情况,学校随机抽查了部分同学周末阅读时间,并且得到数据绘制了不完整的统计图,根据图中信息回答下列问题:
(1)将条形统计图补充完整;被调查的学生周末阅读时间众数是多少小时,中位数是多少小时;
(2)计算被调查学生阅读时间的平均数;
(3)该校八年级共有500人,试估计周末阅读时间不低于1.5小时的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
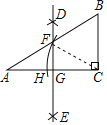
【题目】如图,在△ABC中,∠ACB=90°,分别以点A、C为圆心,以大于![]() AC的长为半径画弧,两弧相交于点D和E,作直线DE交AB于点F,交AC于点G,连接CF,以点C为圆心,以CF的长为半径画弧,交AC于点H.若∠A=30°,BC=2,则AH的长是( )
AC的长为半径画弧,两弧相交于点D和E,作直线DE交AB于点F,交AC于点G,连接CF,以点C为圆心,以CF的长为半径画弧,交AC于点H.若∠A=30°,BC=2,则AH的长是( )
A. ![]() B. 2C.
B. 2C. ![]() +1D. 2
+1D. 2![]() ﹣2
﹣2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com