
【题目】已知如图,在数轴上点![]() ,
, ![]() 所对应的数是
所对应的数是![]() ,
, ![]() .
.
对于关于![]() 的代数式
的代数式![]() ,我们规定:当有理数
,我们规定:当有理数![]() 在数轴上所对应的点为
在数轴上所对应的点为![]() 之间(包括点
之间(包括点![]() ,
, ![]() )的任意一点时,代数式
)的任意一点时,代数式![]() 取得所有值的最大值小于等于
取得所有值的最大值小于等于![]() ,最小值大于等于
,最小值大于等于![]() ,则称代数式
,则称代数式![]() ,是线段
,是线段![]() 的封闭代数式.
的封闭代数式.
例如,对于关于![]() 的代数式
的代数式![]() ,当
,当![]() 时,代数式
时,代数式![]() 取得最大值是
取得最大值是![]() ;当
;当![]() 时,代数式
时,代数式![]() 取得最小值是
取得最小值是![]() ,所以代数式
,所以代数式![]() 是线段
是线段![]() 的封闭代数式.
的封闭代数式.
问题:(![]() )关于
)关于![]() 代数式
代数式![]() ,当有理数
,当有理数![]() 在数轴上所对应的点为
在数轴上所对应的点为![]() 之间(包括点
之间(包括点![]() ,
, ![]() )的任意一点时,取得的最大值和最小值分别是__________.
)的任意一点时,取得的最大值和最小值分别是__________.
所以代数式![]() __________(填是或不是)线段
__________(填是或不是)线段![]() 的封闭代数式.
的封闭代数式.
(![]() )以下关
)以下关![]() 的代数式:
的代数式:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
是线段![]() 的封闭代数式是__________,并证明(只需要证明是线段
的封闭代数式是__________,并证明(只需要证明是线段![]() 的封闭代数式的式子,不是的不需证明).
的封闭代数式的式子,不是的不需证明).
(![]() )关于
)关于![]() 的代数式
的代数式![]() 是线段
是线段![]() 的封闭代数式,则有理数
的封闭代数式,则有理数![]() 的最大值是__________,最小值是__________.
的最大值是__________,最小值是__________.
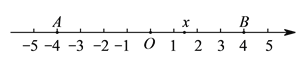
【答案】(![]() )见解析(
)见解析(![]() )④(
)④(![]() )
)![]() ;
; ![]()
【解析】试题分析:(1)观察数轴,当![]() 时,
时, ![]() 取得最大值为
取得最大值为![]() ,当
,当![]() 时,
时, ![]() 取得最小值为
取得最小值为![]() ,所以代数式
,所以代数式![]() 不是线段
不是线段![]() 的封闭代数式;
的封闭代数式;
(2)按照封闭代数式的定义,逐个分析即可;
(3)观察代数式可知,当![]() 时,
时, ![]() 取得最大值为
取得最大值为![]() ,列方程求出x的值;当
,列方程求出x的值;当![]() 时,
时,
![]() 取得最小值为
取得最小值为![]() ,列方程求出x的值;然后从中选出最大的和最小的.
,列方程求出x的值;然后从中选出最大的和最小的.
(![]() )解:当
)解:当![]() 时,
时, ![]() 取得最大值为
取得最大值为![]() ,
,
当![]() 时,
时, ![]() 取得最小值为
取得最小值为![]() ,
,
∵![]() 的最大值
的最大值![]() ,
,
∴![]() 不是线段
不是线段![]() 的封闭代数式.
的封闭代数式.
(![]() )证明:①∵
)证明:①∵ ![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() 的最小值为
的最小值为![]() ,不满足最小值大于等于
,不满足最小值大于等于![]() ,
,
∴![]() 不是线段
不是线段![]() 的封闭代数式.
的封闭代数式.
②当![]() 时,
时,
代数式![]() 取得最大值
取得最大值![]() ,不满足最大值小于等于
,不满足最大值小于等于![]() ,
,
∴![]() 不是线段
不是线段![]() 的封闭代数式.
的封闭代数式.
③当![]() 时,
时,
代数式![]() 取得最大值
取得最大值![]() ,不满足最大值小于等于
,不满足最大值小于等于![]() ,
,
∴![]() 不是线段
不是线段![]() 的封闭代数式.
的封闭代数式.
④当![]() 时,
时,
原式![]()
![]()
![]() ,
,
当![]() 时,
时,
原式![]()
![]()
![]() ,
,
∴![]() ,
,
当![]() 时,
时,
原式![]()
![]()
![]() ,
,
综上所述: ![]() 满足最大值小于等于
满足最大值小于等于![]() ,最小值大于等于
,最小值大于等于![]() ,
,
∴![]() 是线段
是线段![]() 的封闭代数式.
的封闭代数式.
(![]() )当
)当![]() 时,
时,
![]() 取得最大值为
取得最大值为![]() ,
,
则![]() 或
或![]() ,
,
∴![]() 或
或![]() ,
,
当![]() 时,
时,
![]() 取得最小值为
取得最小值为![]() ,
,
则![]() 或
或![]() ,
,
∴![]() 或
或![]() ,
,
综上所述: ![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() .
.
点睛:本题考查了信息迁移类题目的解答,用到了数轴上两点间的距离,解绝对值方程等知识点和分类讨论的数学思想;正确理解“封闭代数式”的意义是解答本题的关键.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为⊙O的内接四边形,且对角线AC为直径,AD=BC,过点D作DG⊥AC,垂足为E,DG分别与AB及CB延长线交于点F、M.
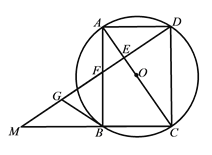
(1)求证:四边形ABCD是矩形;
(2)若点G为MF的中点,求证:BG是⊙O的切线;
(3)若AD=4,CM=9,求四边形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com