
【题目】小丽和小明上山游玩,小丽乘缆车,小明步行,两人相约在山顶的缆车终点会合.已知小明行走到缆车终点的路程是缆车到山顶的线路长的2倍,小丽在小明出发后1小时才乘上缆车,缆车的平均速度为190m/min.设小明出发x min后行走的路程为y m.图中的折线表示小明在整个行走过程中y与x的函数关系.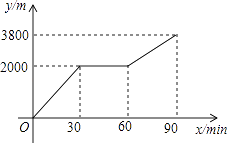
(1)小明行走的总路程是m,他途中休息了min.
(2)①当60≤x≤90时,求y与x的函数关系式;②当小丽到达缆车终点时,小明离缆车终点的路程是多少?
【答案】
(1)3800,30
(2)解:①设当60≤x≤90时,y与x的函数关系式为y=kx+b,
∵图象过点(60,2000),(90,3800),
∴ ![]() ,
,
解得 ![]() ,
,
∴y=60x﹣1600;
②∵小明行走到缆车终点的路程是缆车到山顶的线路长的2倍,小丽在小明出发后1小时才乘上缆车,缆车的平均速度为190m/min,
∴小丽行驶的路程为;3800÷2=1900m,行驶的时间为:1900÷190=10min.
∴小丽到达终点,小明行驶的时间为:60+10=70min.
∴将x=70代入y=60x﹣1600得,y=60×70﹣1600=2600.
∴小明离缆车终点的路程是:3800﹣2600=1200m.
答:小明离缆车终点的路程是1200m
【解析】解:(1)由函数图象,得
小亮行走的总路程是3800米,途中休息了60﹣30=30分钟.
所以答案是:3800,30;
【考点精析】本题主要考查了确定一次函数的表达式的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】我们知道对于x轴上的任意两点A(x1,0),B(x2,0),有AB=|x1﹣x2|,而对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1﹣x2|+|y1﹣y2|称为Pl,P2两点间的直角距离,记作d(P1,P2),即d(P1,P2)=|x1﹣x2|+|y1﹣y2|.
(1)已知O为坐标原点,若点P坐标为(1,3),则d(O,P)= ;
(2)已知O为坐标原点,动点P(x,y)满足d(O,P)=2,请写出x与y之间满足的关系式,并在所给的直角坐标系中画出所有符合条件的点P所组成的图形;
(3)试求点M(2,3)到直线y=x+2的最小直角距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区为了鼓励市民节约用水,计划实行生活用水按阶梯式水价计费,每月用水量不超过10吨(含10吨)时,每吨按基础价收费;每月用水量超过10吨时,超过的部分每吨按调节价收费.例如,第一个月用水16吨,需交水费17.8元,第二个月用水20吨,需交水费23元.
(1)求每吨水的基础价和调节价;
(2)设每月用水量为x吨,应交水费为y元,写出y与x之间的函数关系式;
(3)若某月用水12吨,应交水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点P的坐标为(0,2),直线y= ![]() 与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为( )
与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为( )
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A在x轴的下方,y轴的右侧,到x轴的距离是3,到y轴的距离是2,则点A的坐标是( )
A.(2,﹣3)
B.(2,3)
C.(3,﹣2)
D.(﹣3,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿直线AE折叠,当点D的对应点F刚好落在线段AB的垂直平分线上时,则DE的长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
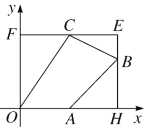
【题目】如图,四边形OABC各个顶点的坐标分别是O(0,0)、A(2,0)、B(4,2)、C(2,3),过点C与![]() 轴平行的直线EF与过点B与
轴平行的直线EF与过点B与![]() 轴平行的直线EH交于点E.
轴平行的直线EH交于点E.
求四边形OABC的面积;
在线段EH上是否存在点P,使四边形OAPC的面积为7?若不存在,说明理由,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列分解因式正确的是( )
A.﹣a+a3=﹣a(1+a2)
B.2a﹣4b+2=2(a﹣2b)
C.a2﹣4=(a﹣2)2
D.a2﹣2a+1=(a﹣1)2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com