
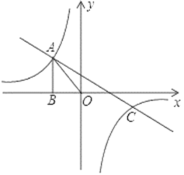
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΖ¥±»άΐΚ· ΐy1ΘΫ![]() ΚΆ“Μ¥ΈΚ· ΐy2ΘΫk2x+bΒΡΆΦœσœύΫΜ”ΎΒψAΓΔCΝΫΒψΘ§Τδ÷–ΒψAΒΡΚαΉχ±ξΈΣ©¹2Θ§ΒψCΒΡΉίΉχ±ξΈΣ©¹1Θ§ΙΐΒψAΉςABΓΆx÷α”ΎΒψBΘ§ΓςAOBΒΡΟφΜΐΈΣ2Θ°
ΚΆ“Μ¥ΈΚ· ΐy2ΘΫk2x+bΒΡΆΦœσœύΫΜ”ΎΒψAΓΔCΝΫΒψΘ§Τδ÷–ΒψAΒΡΚαΉχ±ξΈΣ©¹2Θ§ΒψCΒΡΉίΉχ±ξΈΣ©¹1Θ§ΙΐΒψAΉςABΓΆx÷α”ΎΒψBΘ§ΓςAOBΒΡΟφΜΐΈΣ2Θ°
Θ®1Θ©«σΖ¥±»άΐΚ· ΐΚΆ“Μ¥ΈΚ· ΐΒΡΫβΈω ΫΘ°
Θ®2Θ©ΗυΨίΆΦœσ÷±Ϋ”ΜΊ¥πΘΚΒ±x»ΓΚΈ÷Β ±Θ§“Μ¥ΈΚ· ΐ¥σ”ΎΖ¥±»άΐΚ· ΐΒΡ÷ΒΘ°
Θ®3Θ©»τAΒψΙΊ”Ύx÷αΒΡΕ‘≥ΤΒψAΓδ‘ΎΕΰ¥ΈΚ· ΐy3ΘΫ©¹x2+mx+nΒΡΆΦœσ…œΘ§«κ≈–ΕœΕΰ¥ΈΚ· ΐy4ΘΫx2+mx©¹n©¹3”κx÷αΒΡΫΜΒψΗω ΐΘ§≤ΔΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() Θ§
Θ§![]() ΘΜΘ®2Θ©xΘΦ©¹2Μρ0ΘΦxΘΦ4ΘΜΘ®3Θ©ΝΫΗωΫΜΒψΘ§ΦϊΫβΈω
ΘΜΘ®2Θ©xΘΦ©¹2Μρ0ΘΦxΘΦ4ΘΜΘ®3Θ©ΝΫΗωΫΜΒψΘ§ΦϊΫβΈω
ΓΨΫβΈωΓΩ
(1)ΗυΨίΖ¥±»άΐΚ· ΐ![]() ΒΡΦΗΚΈ“β“εΘ§ΒΟΒΫ
ΒΡΦΗΚΈ“β“εΘ§ΒΟΒΫ![]() =4Θ§ΦΧΕχΒΟΒΫΒΟ
=4Θ§ΦΧΕχΒΟΒΫΒΟ![]() =-4Θ§Ω…«σΒΟAΓΔCΝΫΒψΉχ±ξΘ§¥ζ»κ“Μ¥ΈΚ· ΐΫβΈω ΫΒΟΙΊ”Ύ
=-4Θ§Ω…«σΒΟAΓΔCΝΫΒψΉχ±ξΘ§¥ζ»κ“Μ¥ΈΚ· ΐΫβΈω ΫΒΟΙΊ”Ύ![]() ΓΔbΒΡΕΰ‘Σ“Μ¥ΈΖΫ≥ΧΉιΘ§«σΒΟ“Μ¥ΈΚ· ΐΫβΈω ΫΘΜ
ΓΔbΒΡΕΰ‘Σ“Μ¥ΈΖΫ≥ΧΉιΘ§«σΒΟ“Μ¥ΈΚ· ΐΫβΈω ΫΘΜ
(2)Ιέ≤λΆΦœσΘ§![]() ΘΨ
ΘΨ![]() Θ§Φ¥±μ Ψ
Θ§Φ¥±μ Ψ![]() ΒΡΆΦœσΈΜ”Ύ
ΒΡΆΦœσΈΜ”Ύ![]() ΒΡΆΦœσ…œΖΫΘ§÷±Ϋ”’“≥ωΕ‘”ΠΒΡxΒΡ»Γ÷ΒΖΕΈßΘΜ
ΒΡΆΦœσ…œΖΫΘ§÷±Ϋ”’“≥ωΕ‘”ΠΒΡxΒΡ»Γ÷ΒΖΕΈßΘΜ
(3)”…Χβ“βΩ…ΒΟΒΫn=2m+2Θ§‘ΌΗυΨίΕΰ¥ΈΚ· ΐΆΦœσ”κx÷αΫΜΒψ«ιΩω”κΕ‘”ΠΒΡ“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΗυΒΡ«ιΩω”–ΙΊΘ§«σ≥ω![]() ΒΡ÷ΒΦ¥Ω…≈–ΕœΘ°
ΒΡ÷ΒΦ¥Ω…≈–ΕœΘ°
(1)ΓΏSΓςAOB=2Θ§
Γύ![]() =4Θ§
=4Θ§
ΓΏ![]() ΒΡΆΦœσΈΜ”ΎΒΎΕΰΓΔΥΡœσœόΘ§
ΒΡΆΦœσΈΜ”ΎΒΎΕΰΓΔΥΡœσœόΘ§
Γύ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΓύA(©¹2Θ§2)Θ§C(4Θ§©¹1)Θ§
”…Χβ“βΒΟΘΚ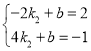 Θ§
Θ§
ΫβΒΟ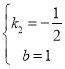 ΘΜ
ΘΜ
Γύ![]() ΘΜ
ΘΜ
(2)Ιέ≤λΆΦœσΒΟΘΚ
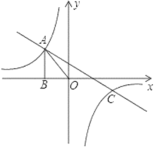
Β±xΘΦ©¹2Μρ0ΘΦxΘΦ4 ±Θ§“Μ¥ΈΚ· ΐΒΡΆΦœσ‘ΎΖ¥±»άΐΚ· ΐΆΦœσΒΡ…œΖΫΘ§
ΓύΒ±xΘΦ©¹2Μρ0ΘΦxΘΦ4 ±Θ§y2ΘΨy1ΘΜ
(3)Βψ A(©¹2Θ§2)ΙΊ”Ύx÷αΒΡΕ‘≥ΤΒψAΓδΒΡΉχ±ξΈΣ(©¹2Θ§©¹2)Θ§
ΗυΨίΧβ“βΘ§ΒψAΓδ (©¹2Θ§©¹2)‘Ύ![]() ΒΡΆΦœσ…œΘ§
ΒΡΆΦœσ…œΘ§
Γύ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
‘Ύ![]() ÷–Θ§Νν
÷–Θ§Νν![]() Θ§ΒΟ
Θ§ΒΟ![]() Θ§
Θ§
Γύ![]()
![]()
![]()
![]() Θ§
Θ§
ΓΏ![]() Θ§
Θ§
Γύ![]() Θ§Φ¥
Θ§Φ¥![]() Θ§
Θ§
ΓύΙΊ”ΎxΒΡ“Μ‘ΣΕΰ¥ΈΖΫ≥Χ![]() ”–ΝΫΗω≤ΜœύΒ»ΒΡ Β ΐΗυΘ§
”–ΝΫΗω≤ΜœύΒ»ΒΡ Β ΐΗυΘ§
Φ¥Εΰ¥ΈΚ· ΐ![]() ΒΡΆΦœσ”κx÷α”–ΝΫΗωΫΜΒψΘ°
ΒΡΆΦœσ”κx÷α”–ΝΫΗωΫΜΒψΘ°


 ΜΞΕ·”Δ”οœΒΝ–¥πΑΗ
ΜΞΕ·”Δ”οœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ”–ΥΡ’≈’ΐΟφΖ÷±π±ξ”– ΐΉ÷©¹1Θ§0Θ§1Θ§2ΒΡ≤ΜΆΗΟςΩ®Τ§Θ§ΥϋΟ«≥ΐ ΐΉ÷ΆβΤδ”ύ»Ϊ≤ΩœύΆ§Θ§œ÷ΫΪΥϋΟ«±≥Οφ≥·…œœ¥Ψυ‘»Θ°
Θ®1Θ©ΥφΜζ≥ι»Γ“Μ’≈Ω®Τ§Θ§«σ≥ιΒΫ ΐΉ÷ΓΑ©¹1Γ±ΒΡΗ≈¬ ΘΜ
Θ®2Θ©ΥφΜζ≥ι»Γ“Μ’≈Ω®Τ§Θ§»ΜΚσ≤ΜΖ≈ΜΊΘ§‘ΌΥφΜζ≥ι»Γ“Μ’≈Ω®Τ§Θ§«κ”ΟΝ–±μΜρΜ≠ ςΉ¥ΆΦΒΡΖΫΖ®«σ≥ωΒΎ“Μ¥Έ≥ιΒΫ ΐΉ÷ΓΑ2Γ±«“ΒΎΕΰ¥Έ≥ιΒΫ ΐΉ÷ΓΑ0Γ±ΒΡΗ≈¬ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
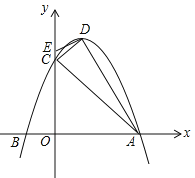
ΓΨΧβΡΩΓΩ“―÷ΣΘ§≈ΉΈοœΏ![]() Θ®aΘΦ0Θ©”κx÷αΫΜ”ΎAΘ®3Θ§0Θ©ΓΔBΝΫΒψΘ§”κy÷αΫΜ”ΎΒψCΘ§≈ΉΈοœΏΒΡΕ‘≥Τ÷α «÷±œΏx=1Θ§DΈΣ≈ΉΈοœΏΒΡΕΞΒψΘ§ΒψE‘Ύy÷αCΒψΒΡ…œΖΫΘ§«“CE=
Θ®aΘΦ0Θ©”κx÷αΫΜ”ΎAΘ®3Θ§0Θ©ΓΔBΝΫΒψΘ§”κy÷αΫΜ”ΎΒψCΘ§≈ΉΈοœΏΒΡΕ‘≥Τ÷α «÷±œΏx=1Θ§DΈΣ≈ΉΈοœΏΒΡΕΞΒψΘ§ΒψE‘Ύy÷αCΒψΒΡ…œΖΫΘ§«“CE=![]() Θ°
Θ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΦΑΕΞΒψDΒΡΉχ±ξΘΜ
Θ®2Θ©«σ÷ΛΘΚ÷±œΏDE «ΓςACDΆβΫ”‘≤ΒΡ«–œΏΘΜ
Θ®3Θ©‘Ύ÷±œΏAC…œΖΫΒΡ≈ΉΈοœΏ…œ’““ΜΒψPΘ§ Ι![]() Θ§«σΒψPΒΡΉχ±ξΘΜ
Θ§«σΒψPΒΡΉχ±ξΘΜ
Θ®4Θ©‘ΎΉχ±ξ÷α…œ’““ΜΒψMΘ§ Ι“‘ΒψBΓΔCΓΔMΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κΓςACDœύΥΤΘ§÷±Ϋ”–¥≥ωΒψMΒΡΉχ±ξΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
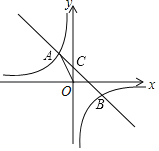
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§“Μ¥ΈΚ· ΐyΘΫax+bΒΡΆΦœσ”κΖ¥±»άΐΚ· ΐyΘΫ![]() Θ®kΈΣ≥Θ ΐΘ§kΓΌ0Θ©ΒΡΆΦœσΫΜ”ΎΕΰΓΔΥΡœσœόΡΎΒΡAΓΔBΝΫΒψΘ§”κy÷αΫΜ”ΎCΒψΘ°ΒψAΒΡΉχ±ξΈΣΘ®mΘ§3Θ©Θ§ΒψB”κΒψAΙΊ”ΎyΘΫx≥…÷αΕ‘≥ΤΘ§tanΓœAOCΘΫ
Θ®kΈΣ≥Θ ΐΘ§kΓΌ0Θ©ΒΡΆΦœσΫΜ”ΎΕΰΓΔΥΡœσœόΡΎΒΡAΓΔBΝΫΒψΘ§”κy÷αΫΜ”ΎCΒψΘ°ΒψAΒΡΉχ±ξΈΣΘ®mΘ§3Θ©Θ§ΒψB”κΒψAΙΊ”ΎyΘΫx≥…÷αΕ‘≥ΤΘ§tanΓœAOCΘΫ![]() Θ°
Θ°
Θ®1Θ©«σkΒΡ÷ΒΘΜ
Θ®2Θ©÷±Ϋ”–¥≥ωΒψBΒΡΉχ±ξΘ§≤Δ«σ÷±œΏABΒΡΫβΈω ΫΘΜ
Θ®3Θ©P «y÷α…œ“ΜΒψΘ§«“SΓςPBCΘΫ2SΓςAOBΘ§«σΒψPΒΡΉχ±ξΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§ΫΪ’ΐΖΫ–Έ![]() »ΤΒψ
»ΤΒψ![]() Ρφ ±’κ–ΐΉΣ
Ρφ ±’κ–ΐΉΣ![]() ΚσΒΟΒΫ’ΐΖΫ–Έ
ΚσΒΟΒΫ’ΐΖΫ–Έ![]() Θ§“ά¥ΥΖΫ ΫΘ§»ΤΒψ
Θ§“ά¥ΥΖΫ ΫΘ§»ΤΒψ![]() Ν§–χ–ΐΉΣ2019¥ΈΒΟΒΫ’ΐΖΫ–Έ
Ν§–χ–ΐΉΣ2019¥ΈΒΟΒΫ’ΐΖΫ–Έ![]() Θ§»γΙϊΒψ
Θ§»γΙϊΒψ![]() ΒΡΉχ±ξΈΣΘ®1Θ§0Θ©Θ§Ρ«Ο¥Βψ
ΒΡΉχ±ξΈΣΘ®1Θ§0Θ©Θ§Ρ«Ο¥Βψ![]() ΒΡΉχ±ξΈΣ________Θ°
ΒΡΉχ±ξΈΣ________Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥Τϊ≥Βœζ έ…ΧΆΤ≥ωΖ÷ΤΎΗΕΩνΙΚ≥Β¥ΌœζΜνΕ·Θ§ΫΜ ΉΗΕΩνΚσΘ§”ύΕν“Σ‘Ύ30Ηω‘¬ΡΎΫα«εΘ§≤ΜΦΤΥψάϊœΔΘ§Άθœ»…ζ‘ΎΜνΕ·ΤΎΦδΙΚ¬ρΝΥΦέΗώΈΣ12Άρ‘ΣΒΡΤϊ≥ΒΘ§ΫΜΝΥ ΉΗΕΩνΚσΤΫΨυΟΩ‘¬ΗΕΩν![]() Άρ‘ΣΘ§
Άρ‘ΣΘ§![]() Ηω‘¬Ϋα«εΘ°
Ηω‘¬Ϋα«εΘ°![]() ”κ
”κ![]() ΒΡΚ· ΐΙΊœΒ»γΆΦΥυ ΨΘ§ΗυΨίΆΦœώΜΊ¥πœ¬Ν–Έ ΧβΘΚ
ΒΡΚ· ΐΙΊœΒ»γΆΦΥυ ΨΘ§ΗυΨίΆΦœώΜΊ¥πœ¬Ν–Έ ΧβΘΚ
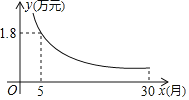
Θ®1Θ©»ΖΕ®![]() ”κ
”κ![]() ΒΡΚ· ΐΫβΈω ΫΘ§≤Δ«σ≥ω ΉΗΕΩνΒΡ ΐΡΩΘΜ
ΒΡΚ· ΐΫβΈω ΫΘ§≤Δ«σ≥ω ΉΗΕΩνΒΡ ΐΡΩΘΜ
Θ®2Θ©Άθœ»…ζ»τ”Ο20Ηω‘¬Ϋα«εΘ§ΤΫΨυΟΩ‘¬”ΠΗΕΕύ…ΌΆρ‘ΣΘΩ
Θ®3Θ©»γΙϊ¥ρΥψΟΩ‘¬ΗΕΩν≤Μ≥§Ιΐ4000‘ΣΘ§Άθœ»…ζ÷Ν…Ό“ΣΦΗΗω‘¬≤≈ΡήΫα«ε”ύΕνΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ―¥ΤΎΒΫά¥Θ§…ΫΚ鱩ΖΔΘ°œ¬±μΦ«¬ΦΝΥΡ≥Υ°Ωβ![]() ΡΎΥ°ΈΜΒΡ±δΜ·«ιΩωΘ§Τδ÷–
ΡΎΥ°ΈΜΒΡ±δΜ·«ιΩωΘ§Τδ÷–![]() ±μ Ψ ±Φδ(ΒΞΈΜΘΚ
±μ Ψ ±Φδ(ΒΞΈΜΘΚ![]() )Θ§
)Θ§![]() ±μ ΨΥ°ΈΜΗΏΕ»(ΒΞΈΜΘΚ
±μ ΨΥ°ΈΜΗΏΕ»(ΒΞΈΜΘΚ![]() )Θ§Β±
)Θ§Β±![]() ±Θ§¥οΒΫΨ·ΫδΥ°ΈΜΘ§ΩΣ ΦΩΣ’ΔΖ≈Υ°Θ°
±Θ§¥οΒΫΨ·ΫδΥ°ΈΜΘ§ΩΣ ΦΩΣ’ΔΖ≈Υ°Θ°
| 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 14 | 15 | 16 | 17 | 18 | 14.4 | 12 | 10.3 | 9 | 8 | 7.2 |

(1)‘ΎΗχ≥ωΒΡΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§ΗυΨί±μΗώ÷–ΒΡ ΐΨίΟη≥ωœύ”ΠΒΡΒψΘ°
(2)«κΖ÷±π«σ≥ωΩΣ’ΔΖ≈Υ°«ΑΚΆΖ≈Υ°ΚσΉνΖϊΚœ±μ÷– ΐΨίΒΡΚ· ΐΫβΈω ΫΘ°
(3)ΨίΙάΦΤΘ§ΩΣ’ΔΖ≈Υ°ΚσΘ§Υ°ΈΜΒΡ’β÷÷±δΜ·Ιφ¬…ΜΙΜα≥÷–χ“ΜΕΈ ±ΦδΘ§‘Λ≤βΚΈ ±Υ°ΈΜ¥οΒΫ![]() Θ°
Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΆθΆ§―ß Ι“Μ≥ΛΈΣ4cmΘ§ΩμΈΣ3cmΒΡ≥ΛΖΫ–ΈΡΨΑεΘ§‘ΎΉάΟφ…œΉωΈόΜ§Ε·ΒΡΖ≠ΙωΘ®Υ≥ ±’κΖΫœρΘ©ΡΨΑε…œΒψAΈΜ÷Ο±δΜ·ΈΣ![]() Θ§Τδ÷–ΒΎΕΰ¥ΈΖ≠Ιω±ΜΉάΟφ…œ“Μ–ΓΡΨΩιΒ≤ΉΓΘ§ ΙΡΨΑε”κΉάΟφ≥…30ΓψΫ«Θ§‘ρΒψAΖ≠ΙωΒΫA2ΈΜ÷Ο ±Ι≤ΉΏΙΐΒΡ¬ΖΨΕ≥ΛΈΣΘ® Θ©
Θ§Τδ÷–ΒΎΕΰ¥ΈΖ≠Ιω±ΜΉάΟφ…œ“Μ–ΓΡΨΩιΒ≤ΉΓΘ§ ΙΡΨΑε”κΉάΟφ≥…30ΓψΫ«Θ§‘ρΒψAΖ≠ΙωΒΫA2ΈΜ÷Ο ±Ι≤ΉΏΙΐΒΡ¬ΖΨΕ≥ΛΈΣΘ® Θ©

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
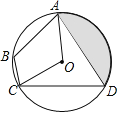
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΓ―OΒΡΑκΨΕΈΣ2Θ§ΥΡ±Ώ–ΈABCD «Γ―OΒΡΡΎΫ”ΥΡ±Ώ–ΈΘ§ΓœABCΘΫΓœAOCΘ§«“ADΘΫCDΘ§‘ρΆΦ÷–“θ”Α≤ΩΖ÷ΒΡΟφΜΐΒ»”Ύ______Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com